5.8. GroupBy (opt)

Prerequisites

• Functions

• pandas introduction 1 and 2

• Reshape

Outcomes

• Understand the split-apply-combine strategy for aggregate computations on groups of data

• Be able use basic aggregation methods on df.groupby to compute within group statistics

• Understand how to group by multiple keys at once

Data

• Details for all delayed US domestic flights in December 2016, obtained from the Bureau of Transportation Statistics

# Uncomment following line to install on colab
#! pip install qeds

import random
import numpy as np
import pandas as pd
import qeds
import matplotlib.pyplot as plt

%matplotlib inline
# activate plot theme
import qeds
qeds.themes.mpl_style();

5.8.1. Outline

• GroupBy

  • Split-Apply-Combine

  • Case Study: Airline Delays

  • Exercise: Cohort Analysis using Shopify Data

  • Exercises

5.8.2. Split-Apply-Combine

One powerful paradigm for analyzing data is the “Split-Apply-Combine” strategy.

This strategy has three steps:

1. Split: split the data into groups based on values in one or more columns.

2. Apply: apply a function or routine to each group separately.

3. Combine: combine the output of the apply step into a DataFrame, using the group identifiers as the index.

We will cover the main components in this lecture, but we encourage you to also study the official documentation to learn more about what is possible.

To describe the concepts, we will need some data.

We will begin with a simple made-up dataset to discuss the concepts and then work through extended example and exercises with real data.

C = np.arange(1, 7, dtype=float)
C[[3, 5]] = np.nan
df = pd.DataFrame({
    "A" : [1, 1, 1, 2, 2, 2],
    "B" : [1, 1, 2, 2, 1, 1],
    "C": C,
})
df

	A	B	C
0	1	1	1.0
1	1	1	2.0
2	1	2	3.0
3	2	2	NaN
4	2	1	5.0
5	2	1	NaN

5.8.2.1. Simple Example

To perform the Split step, we call the groupby method on our DataFrame.

The first argument to groupby is a description of how we want to construct groups.

In the most basic version, we will pass a string identifying the column name.

gbA = df.groupby("A")

The type of variable we get back is a DataFrameGroupBy, which we will sometimes refer to as GroupBy for short.

type(gbA)

pandas.core.groupby.generic.DataFrameGroupBy

Looking at the “groups” inside of the GroupBy object can help us understand what the GroupBy represents.

We can do this with the gb.get_group(group_name) method.

gbA.get_group(1)

	A	B	C
0	1	1	1.0
1	1	1	2.0
2	1	2	3.0

gbA.get_group(2)

	A	B	C
3	2	2	NaN
4	2	1	5.0
5	2	1	NaN

We can apply some of our favorite aggregation functions directly on the GroupBy object.

See exercise 1 in the exercise list

See exercise 2 in the exercise list

If we pass a list of strings to groupby, it will group based on unique combinations of values from all columns in the list.

Let’s see an example.

gbAB = df.groupby(["A", "B"])
type(gbAB)

pandas.core.groupby.generic.DataFrameGroupBy

gbAB.get_group((1, 1))

	A	B	C
0	1	1	1.0
1	1	1	2.0

Notice that we still have a GroupBy object, so we can apply our favorite aggregations.

gbAB.count()

		C
A	B
1	1	2
	2	1
2	1	1
	2	0

Notice that the output is a DataFrame with two levels on the index and a single column C. (Quiz: how do we know it is a DataFrame with one column and not a Series?)

This highlights a principle of how pandas handles the Combine part of the strategy:

The index of the combined DataFrame will be the group identifiers, with one index level per group key.

5.8.2.2. Custom Aggregate Functions

So far, we have been applying built-in aggregations to our GroupBy object.

We can also apply custom aggregations to each group of a GroupBy in two steps:

1. Write our custom aggregation as a Python function.

2. Passing our function as an argument to the .agg method of a GroupBy.

Let’s see an example.

def num_missing(df):
    "Return the number of missing items in each column of df"
    return df.isnull().sum()

We can call this function on our original DataFrame to get the number of missing items in each column.

num_missing(df)

A    0
B    0
C    2
dtype: int64

We can also apply it to a GroupBy object to get the number of missing items in each column for each group.

gbA.agg(num_missing)

	B	C
A
1	0	0.0
2	0	2.0

The key to keep in mind is that the function we pass to agg should take in a DataFrame (or Series) and return a Series (or single value) with one item per column in the original DataFrame.

When the function is called, the data for each group will be passed to our function as a DataFrame (or Series).

5.8.2.3. Transforms: The apply Method

As we saw in the basics lecture, we can apply transforms to DataFrames.

We can do the same with GroupBy objects using the .apply method.

Let’s see an example.

df

	A	B	C
0	1	1	1.0
1	1	1	2.0
2	1	2	3.0
3	2	2	NaN
4	2	1	5.0
5	2	1	NaN

def smallest_by_b(df):
    return df.nsmallest(2, "B")

gbA.apply(smallest_by_b)

		A	B	C
A
1	0	1	1	1.0
	1	1	1	2.0
2	4	2	1	5.0
	5	2	1	NaN

Notice that the return value from applying our series transform to gbA was the group key on the outer level (the A column) and the original index from df on the inner level.

The original index came along because that was the index of the DataFrame returned by smallest_by_b.

Had our function returned something other than the index from df, that would appear in the result of the call to .apply.

See exercise 3 in the exercise list

5.8.2.4. pd.Grouper

Sometimes, in order to construct the groups you want, you need to give pandas more information than just a column name.

Some examples are:

• Grouping by a column and a level of the index.

• Grouping time series data at a particular frequency.

pandas lets you do this through the pd.Grouper type.

To see it in action, let’s make a copy of df with A moved to the index and a Date column added.

df2 = df.copy()
df2["Date"] = pd.date_range(
    start=pd.datetime.today().strftime("%m/%d/%Y"),
    freq="BQ",
    periods=df.shape[0]
)
df2 = df2.set_index("A")
df2

	B	C	Date
A
1	1	1.0	2020-09-30
1	1	2.0	2020-12-31
1	2	3.0	2021-03-31
2	2	NaN	2021-06-30
2	1	5.0	2021-09-30
2	1	NaN	2021-12-31

We can group by year.

df2.groupby(pd.Grouper(key="Date", freq="A")).count()

	B	C
Date
2020-12-31	2	2
2021-12-31	4	2

We can group by the A level of the index.

df2.groupby(pd.Grouper(level="A")).count()

	B	C	Date
A
1	3	3	3
2	3	1	3

We can combine these to group by both.

df2.groupby([pd.Grouper(key="Date", freq="A"), pd.Grouper(level="A")]).count()

		B	C
Date	A
2020-12-31	1	2	2
2021-12-31	1	1	1
	2	3	1

And we can combine pd.Grouper with a string, where the string denotes a column name

df2.groupby([pd.Grouper(key="Date", freq="A"), "B"]).count()

		C
Date	B
2020-12-31	1	2
2021-12-31	1	1
	2	1

5.8.3. Case Study: Airline Delays

Let’s apply our new split-apply-combine skills to the airline dataset we saw in the merge lecture.

air_dec = qeds.load("airline_performance_dec16")

First, we compute the average delay in arrival time for all carriers each week.

weekly_delays = (
    air_dec
    .groupby([pd.Grouper(key="Date", freq="W"), "Carrier"])
    ["ArrDelay"]               # extract one column
    .mean()                    # take average
    .unstack(level="Carrier")  # Flip carrier up as column names
)
weekly_delays

Carrier	AA	AS	B6	DL	EV	F9	HA	NK	OO	UA	VX	WN
Date
2016-12-04	-1.714887	2.724273	-2.894269	-5.088351	8.655332	-2.894212	-0.558282	5.468909	2.749573	5.564496	-2.121821	-1.663695
2016-12-11	1.148833	12.052031	5.795062	2.507745	13.220673	4.578861	2.054302	8.713755	15.429660	4.094176	12.080938	1.865933
2016-12-18	16.357561	7.643767	34.608356	18.000000	23.876622	45.014888	9.388889	22.857899	30.901639	22.398130	33.651128	18.373400
2016-12-25	6.364513	2.719699	5.586836	-0.916113	6.857143	54.084959	5.075747	10.443369	15.004780	5.332474	17.286917	10.197685
2017-01-01	2.321836	1.226662	10.661577	2.048116	6.800898	8.280298	6.970016	8.361123	8.971083	0.061786	1.349580	5.213019

Let’s also plot this data.

# plot
axs = weekly_delays.plot.bar(
    figsize=(10, 8), subplots=True, legend=False, sharex=True,
    sharey=True, layout=(4, 3), grid=False
)

# tweak spacing between subplots and xaxis labels
axs[0,0].get_figure().tight_layout()
for ax in axs[-1, :]:
    ax.set_xticklabels(weekly_delays.index.strftime("%a, %b. %d'"))

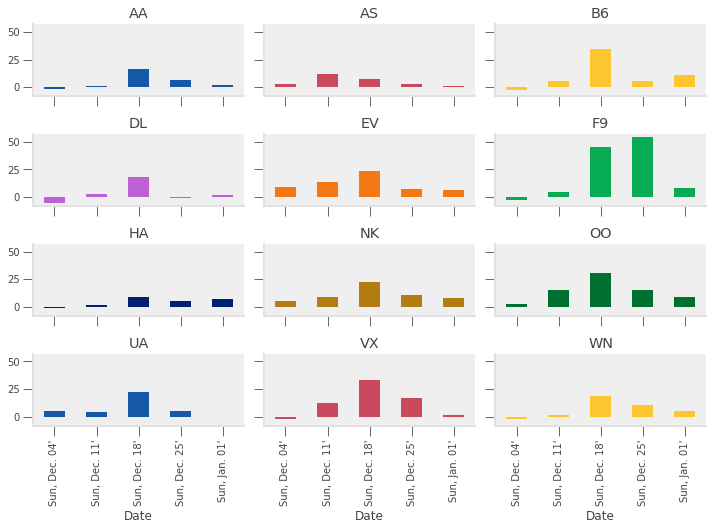
It looks like more delays occurred during the week ending Sunday December 18th than any other week (except for Frontier, who did worse on Christmas week).

Let’s see why.

The air_dec DataFrame has information on the minutes of delay attributed to 5 different categories:

delay_cols = [
    'CarrierDelay',
    'WeatherDelay',
    'NASDelay',
    'SecurityDelay',
    'LateAircraftDelay'
]

Let’s take a quick look at each of those delay categories for the week ending December 18, 2016.

pre_christmas = air_dec.loc[
    (air_dec["Date"] >= "2016-12-12") & (air_dec["Date"] <= "2016-12-18")
]

# custom agg function
def positive(df):
    return (df > 0).sum()

delay_totals = pre_christmas.groupby("Carrier")[delay_cols].agg(["sum", "mean", positive])
delay_totals

	CarrierDelay			WeatherDelay			NASDelay			SecurityDelay			LateAircraftDelay
	sum	mean	positive	sum	mean	positive	sum	mean	positive	sum	mean	positive	sum	mean	positive
Carrier
AA	105732.0	6.258553	2922.0	21820.0	1.291583	456.0	77279.0	4.574346	3159.0	721.0	0.042678	35.0	141249.0	8.360897	2574.0
AS	8762.0	2.691032	250.0	3219.0	0.988636	61.0	16344.0	5.019656	614.0	163.0	0.050061	10.0	13599.0	4.176597	271.0
B6	49421.0	9.031615	1575.0	9894.0	1.808114	112.0	38741.0	7.079861	1326.0	672.0	0.122807	30.0	100811.0	18.423063	1433.0
DL	151188.0	8.864212	2878.0	39145.0	2.295087	783.0	75110.0	4.403729	2605.0	107.0	0.006273	2.0	122896.0	7.205441	2289.0
EV	87408.0	9.939504	1375.0	3824.0	0.434842	76.0	49703.0	5.651922	1580.0	0.0	0.000000	0.0	89773.0	10.208438	1568.0
F9	19568.0	10.430704	361.0	6198.0	3.303838	57.0	22459.0	11.971748	493.0	0.0	0.000000	0.0	32236.0	17.183369	316.0
HA	7199.0	5.034266	218.0	3650.0	2.552448	145.0	86.0	0.060140	4.0	35.0	0.024476	3.0	4024.0	2.813986	189.0
NK	14735.0	5.294646	452.0	2240.0	0.804887	56.0	30361.0	10.909450	840.0	50.0	0.017966	5.0	22247.0	7.993891	372.0
OO	120307.0	10.439691	1378.0	26349.0	2.286446	308.0	54141.0	4.698108	2289.0	171.0	0.014839	12.0	166102.0	14.413572	2459.0
UA	66693.0	6.312636	1851.0	31602.0	2.991197	521.0	74992.0	7.098154	2065.0	0.0	0.000000	0.0	118728.0	11.237861	1696.0
VX	8048.0	5.608362	246.0	3807.0	2.652962	126.0	12619.0	8.793728	224.0	73.0	0.050871	4.0	25242.0	17.590244	331.0
WN	123882.0	4.873790	5393.0	23516.0	0.925171	328.0	78645.0	3.094067	4247.0	252.0	0.009914	18.0	285073.0	11.215399	6472.0

Want: plot total, average, and number of each type of delay by carrier

To do this, we need to have a DataFrame with:

• Delay type in index (so it is on horizontal-axis)

• Aggregation method on outer most level of columns (so we can do data["mean"] to get averages)

• Carrier name on inner level of columns

Many sequences of the reshaping commands can accomplish this.

We show one example below.

reshaped_delays = (
    delay_totals
    .stack()             # move aggregation method into index (with Carrier)
    .T                   # put delay type in index and Carrier+agg in column
    .swaplevel(axis=1)   # make agg method outer level of column label
    .sort_index(axis=1)  # sort column labels so it prints nicely
)
reshaped_delays

	mean										...	sum
Carrier	AA	AS	B6	DL	EV	F9	HA	NK	OO	UA	...	B6	DL	EV	F9	HA	NK	OO	UA	VX	WN
CarrierDelay	6.258553	2.691032	9.031615	8.864212	9.939504	10.430704	5.034266	5.294646	10.439691	6.312636	...	49421.0	151188.0	87408.0	19568.0	7199.0	14735.0	120307.0	66693.0	8048.0	123882.0
WeatherDelay	1.291583	0.988636	1.808114	2.295087	0.434842	3.303838	2.552448	0.804887	2.286446	2.991197	...	9894.0	39145.0	3824.0	6198.0	3650.0	2240.0	26349.0	31602.0	3807.0	23516.0
NASDelay	4.574346	5.019656	7.079861	4.403729	5.651922	11.971748	0.060140	10.909450	4.698108	7.098154	...	38741.0	75110.0	49703.0	22459.0	86.0	30361.0	54141.0	74992.0	12619.0	78645.0
SecurityDelay	0.042678	0.050061	0.122807	0.006273	0.000000	0.000000	0.024476	0.017966	0.014839	0.000000	...	672.0	107.0	0.0	0.0	35.0	50.0	171.0	0.0	73.0	252.0
LateAircraftDelay	8.360897	4.176597	18.423063	7.205441	10.208438	17.183369	2.813986	7.993891	14.413572	11.237861	...	100811.0	122896.0	89773.0	32236.0	4024.0	22247.0	166102.0	118728.0	25242.0	285073.0

5 rows × 36 columns

for agg in ["mean", "sum", "positive"]:
    axs = reshaped_delays[agg].plot(
        kind="bar", subplots=True, layout=(4, 3), figsize=(10, 8), legend=False,
        sharex=True, sharey=True
    )
    fig = axs[0, 0].get_figure()
    fig.suptitle(agg)
#     fig.tight_layout();

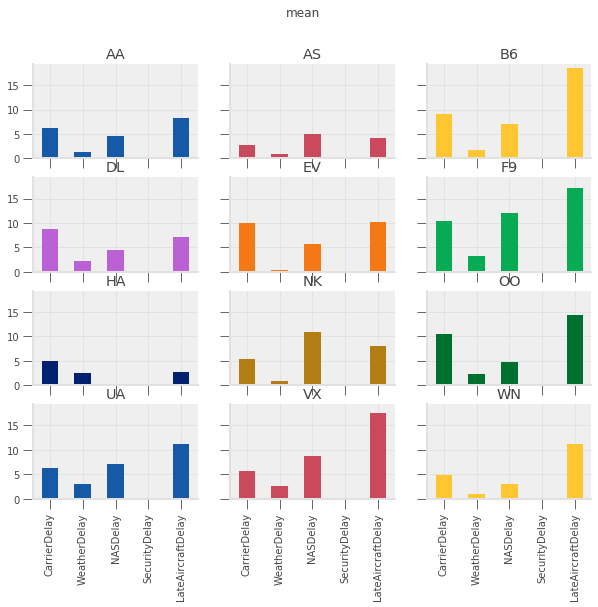
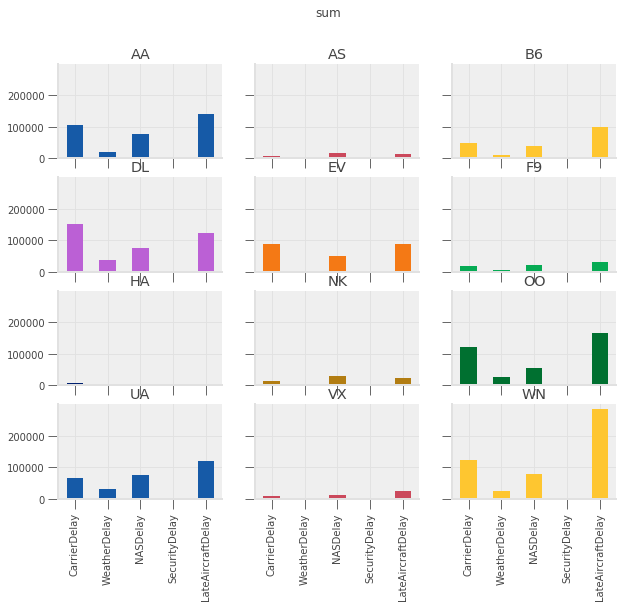
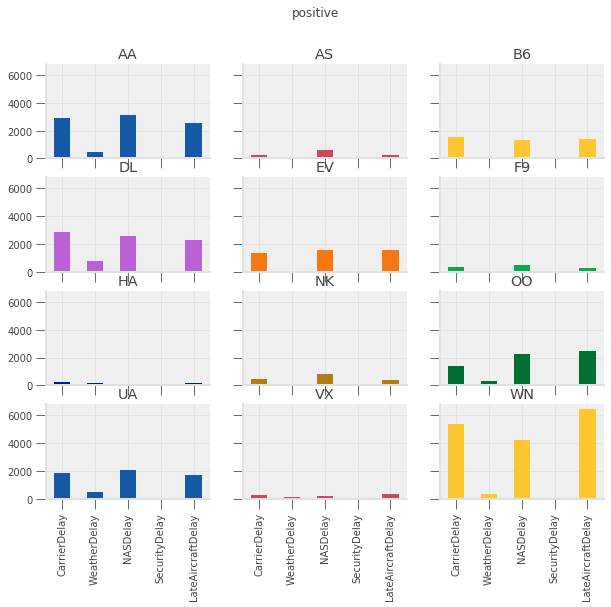
See exercise 4 in the exercise list

Let’s summarize what we did:

• Computed average flight delay for each airline for each week.

• Noticed that one week had more delays for all airlines.

• Studied the flights in that week to determine the cause of the delays in that week.

Suppose now that we want to repeat that analysis, but at a daily frequency instead of weekly.

We could copy/paste the code from above and change the W to a D, but there’s a better way…

Let’s convert the steps above into two functions:

1. Produce the set of bar charts for average delays at each frequency.

2. Produce the second set of charts for the total, average, and number of occurrences of each type of delay.

def mean_delay_plot(df, freq, figsize=(10, 8)):
    """
    Make a bar chart of average flight delays for each carrier at
    a given frequency.
    """
    mean_delays = (
        df
        .groupby([pd.Grouper(key="Date", freq=freq), "Carrier"])
        ["ArrDelay"]               # extract one column
        .mean()                    # take average
        .unstack(level="Carrier")  # Flip carrier up as column names
    )

    # plot
    axs = mean_delays.plot.bar(
        figsize=figsize, subplots=True, legend=False, sharex=True,
        sharey=True, layout=(4, 3), grid=False
    )

    # tweak spacing between subplots and x-axis labels
    axs[0, 0].get_figure().tight_layout()
    for ax in axs[-1, :]:
        ax.set_xticklabels(mean_delays.index.strftime("%a, %b. %d'"))

    # return the axes in case we want to further tweak the plot outside the function
    return axs


def delay_type_plot(df, start, end):
    """
    Make bar charts for total minutes, average minutes, and number of
    occurrences for each delay type, for all flights that were scheduled
    between `start` date and `end` date
    """
    sub_df = df.loc[
        (df["Date"] >= start) & (df["Date"] <= end)
    ]

    def positive(df):
        return (df > 0).sum()

    aggs = sub_df.groupby("Carrier")[delay_cols].agg(["sum", "mean", positive])

    reshaped = aggs.stack().T.swaplevel(axis=1).sort_index(axis=1)

    for agg in ["mean", "sum", "positive"]:
        axs = reshaped[agg].plot(
            kind="bar", subplots=True, layout=(4, 3), figsize=(10, 8), legend=False,
            sharex=True, sharey=True
        )
        fig = axs[0, 0].get_figure()
        fig.suptitle(agg)
#         fig.tight_layout();

See exercise 5 in the exercise list

Now let’s look at that plot at a daily frequency. (Note that we need the figure to be a bit wider in order to see the dates.)

mean_delay_plot(air_dec, "D", figsize=(16, 8));

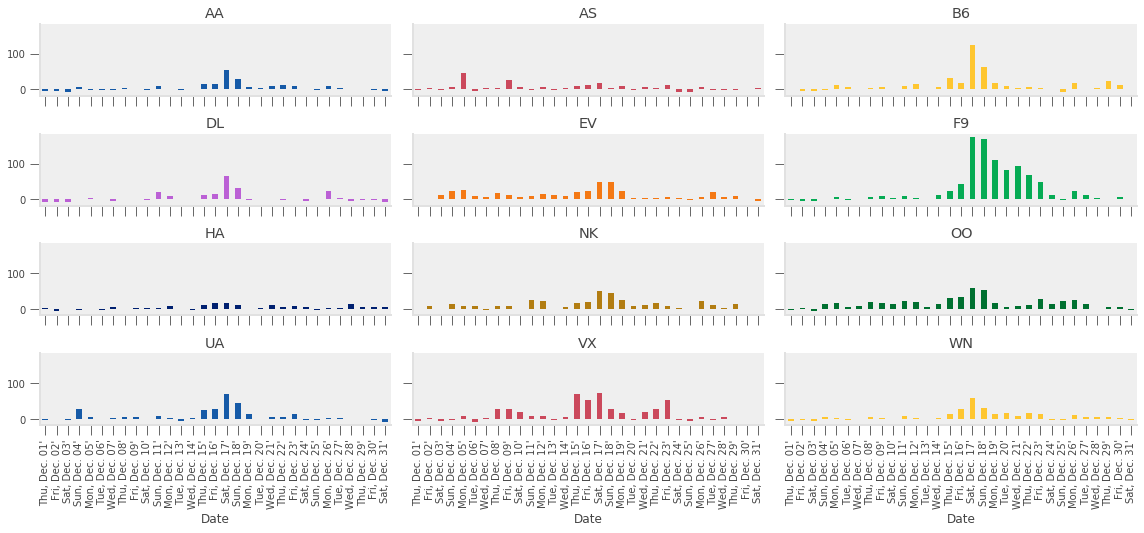
As we expected given our analysis above, the longest average delays seemed to happen in the third week.

In particular, it looks like December 17th and 18th had — on average — higher delays than other days in December.

Let’s use the delay_type_plot function to determine the cause of the delays on those two days.

Because our analysis is captured in a single function, we can look at the days together and separately without much effort.

# both days
delay_type_plot(air_dec, "12-17-16", "12-18-16")

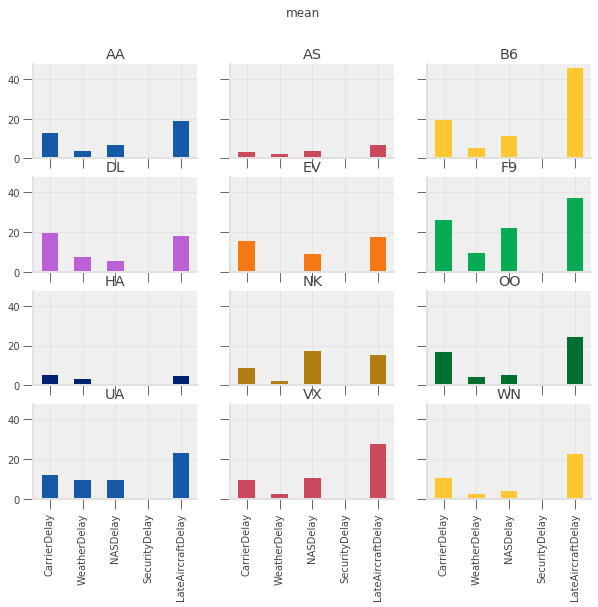
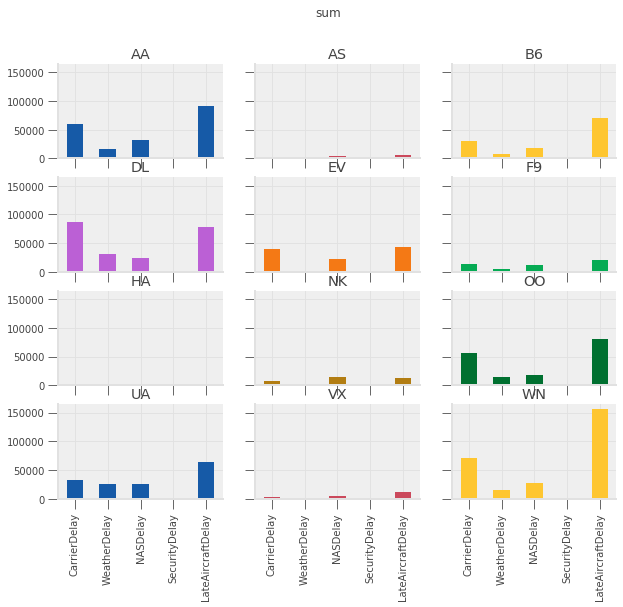
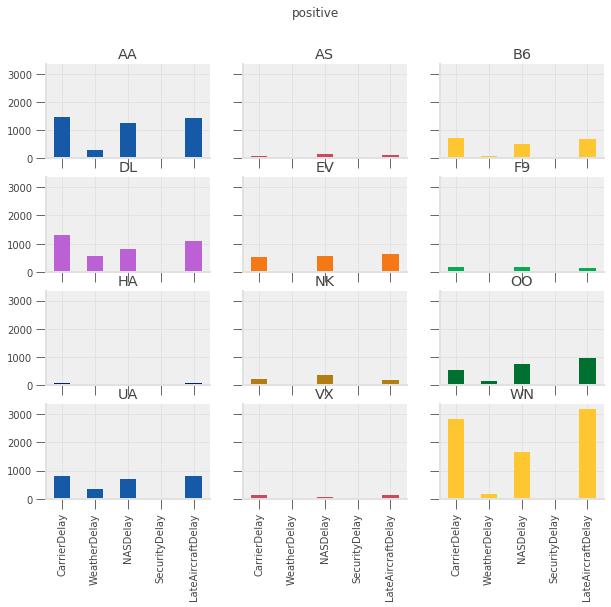
# only the 17th
delay_type_plot(air_dec, "12-17-16", "12-17-16")

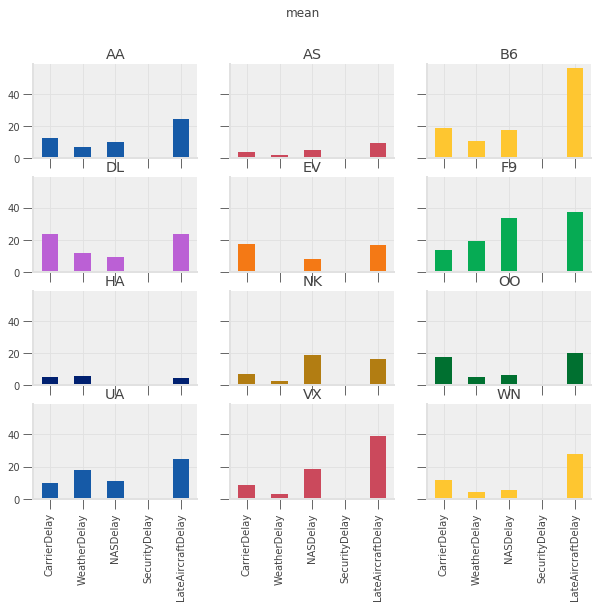
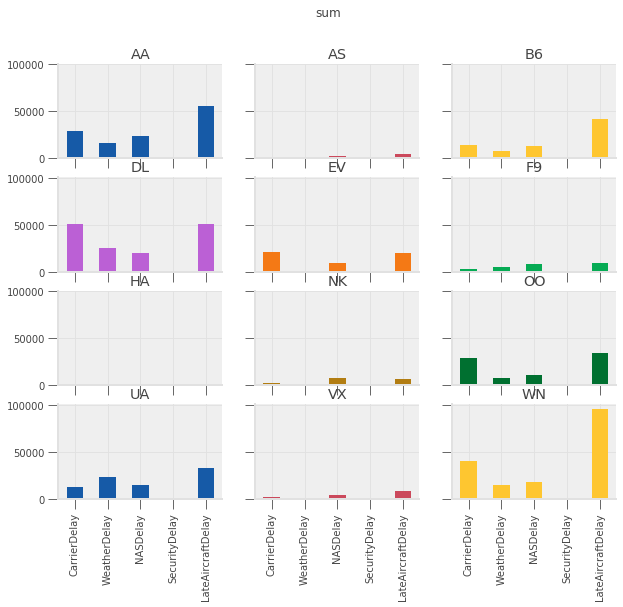
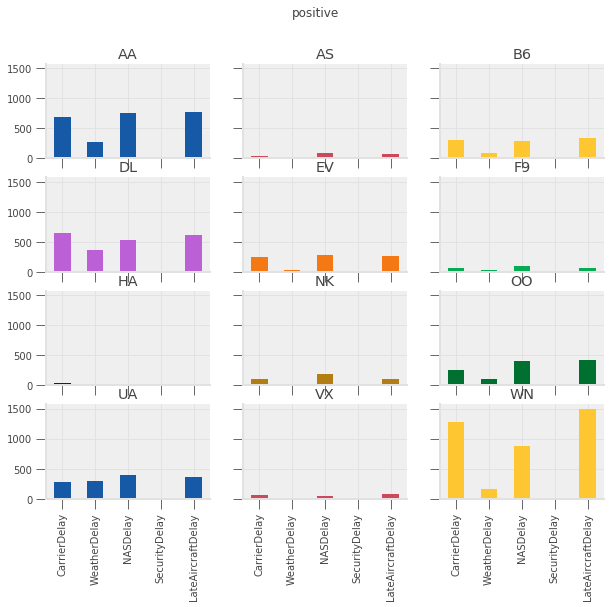
# only the 18th
delay_type_plot(air_dec, "12-18-16", "12-18-16")

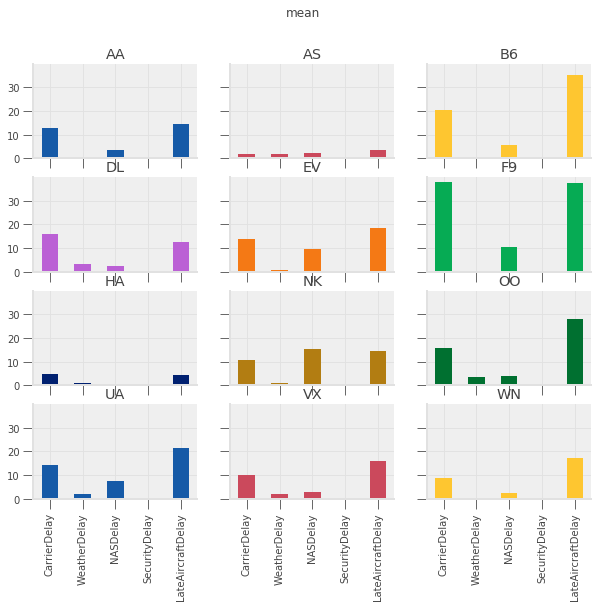
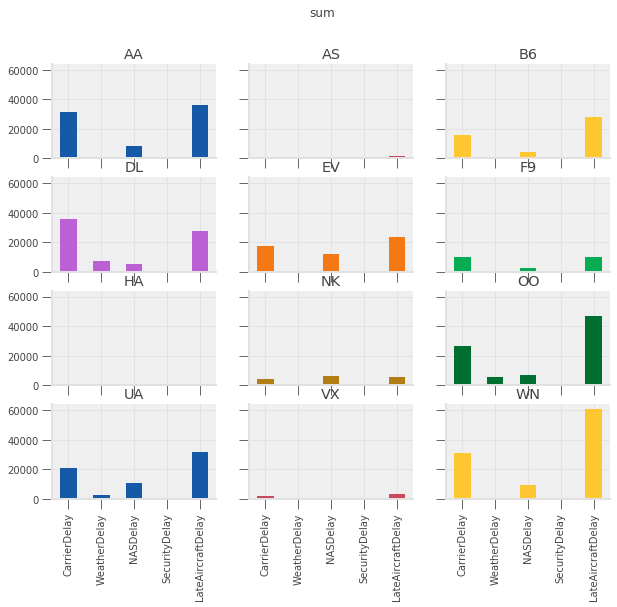
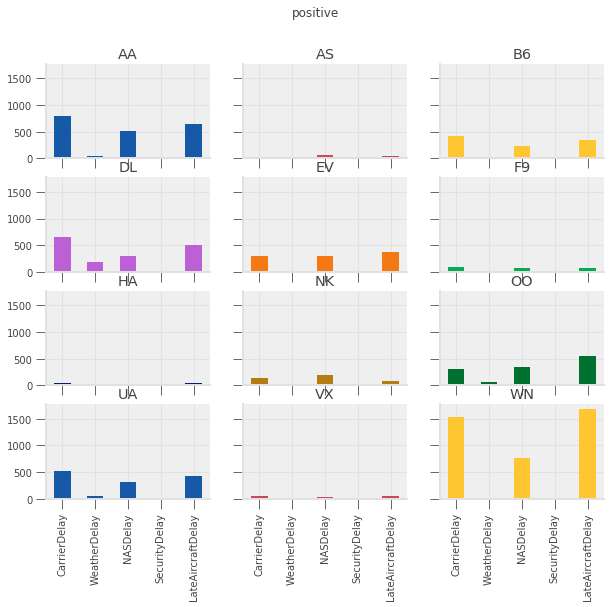
The purpose of this exercise was to drive home the ability to automate tasks.

We were able to write a pair of functions that allows us to easily repeat the exact same analysis on different subsets of the data, or different datasets entirely (e.g. we could do the same analysis on November 2016 data, with two lines of code).

These principles can be applied in many settings.

Keep that in mind as we work through the rest of the materials.

5.8.4. Exercise: Cohort Analysis using Shopify Data

The qeds library includes routines to simulate data sets in the format of common sources

One of these sources is Shopify — an e-commerce platform used by many retail companies for online sales

The code below will simulate a fairly large data set that has the properties of a order-detail report from Shopify

We’ll first look at the data, and then describe the exercise

# Set the "randomness" seeds
random.seed(42)
np.random.seed(42)

orders = qeds.data.shopify.simulate_orders(500000)
orders.info()

orders.head()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 501522 entries, 0 to 501521
Data columns (total 14 columns):
Day                  501522 non-null object
customer_type        501522 non-null object
Customer ID          501522 non-null int64
orders               501522 non-null int64
total_sales          501522 non-null float64
Returns              501522 non-null float64
Ordered quantity     501522 non-null int64
Gross sales          501522 non-null float64
Net sales            501522 non-null float64
Shipping             501522 non-null float64
Tax                  501522 non-null float64
Net quantity         501522 non-null int64
Returned quantity    501522 non-null int64
Discounts            501522 non-null float64
dtypes: float64(7), int64(5), object(2)
memory usage: 53.6+ MB

	Day	customer_type	Customer ID	orders	total_sales	Returns	Ordered quantity	Gross sales	Net sales	Shipping	Tax	Net quantity	Returned quantity	Discounts
0	2020-01-06	Returning	1825044237	1	66.02	-0.0	7	66.02	66.02	0.0	0.00	7	0	-0.0
1	2015-11-08	Returning	5738410335	1	3.91	-0.0	2	3.45	3.45	0.0	0.46	2	0	-0.0
2	2015-01-09	First-time	8183772638	1	62.25	-0.0	7	62.25	62.25	0.0	0.00	7	0	-0.0
3	2014-04-22	First-time	661927852	1	153.78	-0.0	3	153.78	153.78	0.0	0.00	3	0	-0.0
4	2020-03-17	Returning	5481518024	1	13.51	-0.0	1	13.51	13.51	0.0	0.00	1	0	-0.0

We define a customer’s cohort as the month in which a customer placed their first order and the customer type as an indicator of whether this was their first order or a returning order.

We now describe the want for the exercise, which we ask you to complete.

Want: Compute the monthly total number of orders, total sales, and total quantity separated by customer cohort and customer type.

Read that carefully one more time…

5.8.4.1. Extended Exercise

Using the reshape and groupby tools you have learned, apply the want operator described above.

See below for advice on how to proceed.

When you are finished, you should have something that looks like this:

Two notes on the table above:

Your actual output will be much bigger. This is just to give you an

idea of what it might look like.

The numbers you produce should actually be the same as what are

included in this table… Index into your answer and compare what you have with this table to verify your progress.

Now, how to do it?

There is more than one way to code this, but here are some suggested steps.

1. Convert the Day column to have a datetime dtype instead of object (Hint: use the pd.to_datetime function).

2. Add a new column that specifies the date associated with each customer’s "First-time" order.

• Hint 1: You can do this with a combination of groupby and join.

• Hint 2: customer_type is always one of Returning and First-time.

• Hint 3: Some customers don’t have a customer_type == "First-time" entry. You will need to set the value for these users to some date that precedes the dates in the sample. After adding valid data back into orders DataFrame, you can identify which customers don’t have a "First-Time" entry by checking for missing data in the new column.

1. You’ll need to group by 3 things.

2. You can apply one of the built-in aggregation functions to the GroupBy.

3. After doing the aggregation, you’ll need to use your reshaping skills to move things to the right place in rows and columns.

Good luck!

5.8.5. Exercises

Exercise 1

Look closely at the output of the cells below.

How did pandas compute the sum of gbA? What happened to the NaN entries in column C?

Write your thoughts.

Hint: try gbA.count() or gbA.mean() if you can’t decide what happened to the NaN.

df

	A	B	C
0	1	1	1.0
1	1	1	2.0
2	1	2	3.0
3	2	2	NaN
4	2	1	5.0
5	2	1	NaN

gbA.sum()

	B	C
A
1	4	6.0
2	4	5.0

(back to text)

Exercise 2

Use introspection (tab completion) to see what other aggregations are defined for GroupBy objects.

Pick three and evaluate them in the cells below.

Does the output of each of these commands have the same features as the output of gbA.sum() from above? If not, what is different?

# method 1

# method 2

# method 3

(back to text)

Exercise 3

This exercise has a few steps:

1. Write a function that, given a DataFrame, computes each entry’s deviation from the mean of its column.

2. Apply the function to gbA.

3. With your neighbor describe what the index and and columns are? Where are the group keys (the A column)?

4. Determine the correct way to add these results back into df as new columns. (Hint: remember the merge lecture)

# write function here


# apply function here

# add output of function as new columns to df here...

Note that if the group keys

remained in the index as the `.apply`'s output, the merge/join step would have been complicated.

(back to text)

Exercise 4

Think about what is shown in the the plots above.

Answer questions like:

• Which type of delay was the most common?

• Which one caused the largest average delay?

• Does that vary by airline?

Write your thoughts.

# your code here if needed

(back to text)

Exercise 5

Verify that we wrote the functions properly by setting the arguments to appropriate values to replicate the plots from above.

# call mean_delay_plot here

# call delay_type_plot here

(back to text)