import numpy as np
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt

14.4. Multi-factor models#

Adding factors to proxy for the total wealth portfolio

  • According to the CAPM the Wealth portfolio is the tangency portfolio

  • The return on the wealth portfolio summarizes how Bad the times are

  • Assets that co-vary more with the market must earn higher returns

  • They pay poorly exactly when things are worse

  • What is the wealth portfolio? It is the portfolio that holds all assets in proportion to their value

  • We often use the equity market as a proxy for this, but that is not the CAPM

  • In a way that CAPM is untestable because it is impossible to construct the true wealth portfolio

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]\]

  • The fact that we cannot really measure the returns of the total wealth protfolio gives us a reason to add other facts in additons to the returns to the equity market. Under this logic you add returns to other assets classes>

    • Real estate

    • Corporate debt

    • Human capital

    • Private equity

    • Venture Capital -…

So you get:

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]+\sum_a^A\beta_{i,a}E[R^{a}_t-R^f_t]\]

  • where \(a\) are the different asset classes.

  • Sometimes people refer to these other hard to trade assets as “background risks”, basically risks that are you are exposed to that are not capture by your financial assets

ICAPM: Intertemporal Capital Asset Pricing Model

  • Another way to rationalize additional factors is to realize that the premium and the volatiltiy of the market are time-varying.

  • This means that assets that allow you to hedge this investment opportunity set risk will be valuable

    • For example, an asset that pays well when the market is more/less volatile or one that pays well when the expected reutrns of market going froward are higher/lower

  • Under this logic, any strategy that is related to the market moments can also explain average returns on top of the marker beta

  • Sometimes people refer to the background risks discussed earlier in this framework as well. But in this case it is not about the moments of the market portfolio per se, but about correlation of the strategy with the background risks investors bear

  • The end result is the same

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]+\sum_{j=1}^J\beta_{i,j}E[Factor^j_t]\]

  • but now these are “Factors” and do no need to be components of the total wealth

  • but these factors must still be excess returns, i.e. they must be strategies based on financial assets that have price zero

APT: Arbitrage Pricing Theory

  • Yet another model that has exaclty the same prediction

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]+\sum_{j=1}^J\beta_{i,j}E[Factor^j_t]\]

  • but now the factors are motivated because the explain time-seires variation in realized return

  • the idea is that if you have enough factors you explain enough of the variaiton in the returns of an asset that if the betas do no explain the average reuturns than an arbitrage opportunity wouldd open up

  • So you can think of the first two moticaiton being more about “economic factors” while this one being abotu “fianncail factors”. The factors belong if they help you explain reuturs.

  • APT in the end is a very statistical model

How to work with multifactor models?

  • These models make less restrictive assumptions and predict that we will need additional factors beyond the market to “span” the tangency portfolio

  • What does “span” mean?

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]+\sum_{j=1}^J\beta_{i,j}E[Factor^j_t]\]

  • It is basically the same as before, but now we run a multivariate regression

    \[R_{i,t}=\alpha_i+\beta_{mkt}R^{mkt}_t+\beta_1 Factor_1+\beta_2 Factor_2+\beta_3 Factor_3+....+\beta_n Factor_n+\epsilon_{i,t}\]

  • As long as the factors are also excess returns, the time-series alpha test is still valid and indentical as before.

  • You can do single asset tests and simply use the alpha t-stat to test the model

  • Everything that we discussed with the hedging/tracking portfolios apply here as well, but now

\[Hedged_{i,t}=R_{i,t}-(\beta_{mkt}R^{mkt}_t+\beta_1 Factor_1+\beta_2 Factor_2+\beta_3 Factor_3+....+\beta_n Factor_n)\]

where \((\beta_{mkt}R^{mkt}_t+\beta_1 Factor_1+\beta_2 Factor_2+\beta_3 Factor_3+....+\beta_n Factor_n)\) is the tracking portfolio

Which Multi-factor models?

It really depends on the application. Practicioners ofen use factor models with 10 or more factors becasue they are interested in peformance attibution.

You use the regression to see which factor explain some particular realized performance while not thinking to much about whether the factor there explains average returns.

This is a perferctly good use mulitfactor models. In this case you are not really thinking whether the factors help you span the tangency portfolio, but only if it help explain the realized reutrn of the strategy.

If you interesting in accounting for a fund/strategy/stock averagare return you have look for factors that help you span the tangency portfolio, i.e. facots that generate high sharpe ratios.

In the academic world and also in a good chunk of practicioners people use the following factor models

  1. Fama French 3 factor model:

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]+\beta_{i,smb}E[SmB_t]+\beta_{i,HmL}E[HmL_t]\]

  1. Carhart 4 factor model:

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]+\beta_{i,smb}E[SmB_t]+\beta_{i,HmL}E[HmL_t]+\beta_{i,WmL}E[WmL_t]\]

  1. Fama French 5 factor model:

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]+\beta_{i,smb}E[SmB_t]+\beta_{i,HmL}E[HmL_t]+\beta_{i,rmw}E[RmW_t]+\beta_{i,cma}E[CmA_t]\]

  1. Fama French 5 factor model + Momentum:

\[E[R_t^i-R_t^f]=\beta_{i,mkt}E[R^{mkt}_t-R^f_t]+\beta_{i,smb}E[SmB_t]+\beta_{i,HmL}E[HmL_t]+\beta_{i,rmw}E[RmW_t]+\beta_{i,cma}E[CmA_t]+\beta_{i,WmL}E[WmL_t]\]

Where :

  • HmL is the value strategy that buys high book to market firms and sell low book to market firms

  • SmB is a size strategy that buys firms with low market capitalization and sell firms with high market capitalizations

  • WmL is the momentum strategy that buy stocks that did well in the last 12 months and short the ones that did poorly

  • RmW is the strategy that buys firms with high gross proftiability and sell firms with low gross profitability

  • CmA is the strategy that buys firms that are investing little (low CAPEX) and sell firms that are investing a lot (high CAPEX)

Three applications to evalauting asset managers

We will do this in three steps

  1. Get time-series of the factors in our factor model and the risk-free rate

  2. For each application get the time-series return data of the asset being evaluated

  3. Merge with factor series

  4. Convert the returns of the asset being evaluate to excess returns

  5. Run a time-series regression of the asset excess returns on the relevant factors

Factors for our factor model

  • We will start by dowloading he Five factors from Fama Frency 5 factors model plus the momentum factor which is in separate data set

  • We of course could have constructed them ourselves as well, but this is obviously faster and less error prone

from datetime import datetime
import pandas_datareader.data as web
start = datetime(1926, 1, 1)
ds = web.DataReader('F-F_Research_Data_5_Factors_2x3', 'famafrench',start=start)
dff5=ds[0][:'2021-3']
dff5
ds = web.DataReader('F-F_Momentum_Factor', 'famafrench',start=start)
dmom=ds[0][:'2021-3']
dmom
dff6=dff5.merge(dmom,left_index=True,right_index=True,how='inner')
dff6
Mkt-RF SMB HML RMW CMA RF Mom
Date
1963-07 -0.39 -0.45 -0.94 0.66 -1.15 0.27 1.00
1963-08 5.07 -0.82 1.82 0.40 -0.40 0.25 1.03
1963-09 -1.57 -0.48 0.17 -0.76 0.24 0.27 0.16
1963-10 2.53 -1.30 -0.04 2.75 -2.24 0.29 3.14
1963-11 -0.85 -0.85 1.70 -0.45 2.22 0.27 -0.75
... ... ... ... ... ... ... ...
2020-11 12.47 6.75 2.11 -2.78 1.05 0.01 -12.25
2020-12 4.63 4.67 -1.36 -2.15 0.00 0.01 -2.42
2021-01 -0.03 6.88 2.85 -3.33 4.68 0.00 4.37
2021-02 2.78 4.51 7.08 0.09 -1.97 0.00 -7.68
2021-03 3.09 -0.98 7.40 6.43 3.44 0.00 -5.83

693 rows × 7 columns

Aplication 1: Performance evaluation of Berkshire Hathaway

  • How much of WB performance can be explained by his exposure to the differnet risk factors?

  • How much of WB performance is due to his ability to buy good business for cheap?

Getting the Data

We will do the data at monthly frequency.

While daily data is helpful in estiamting betas we have do be mindful of liqudiity effects, for example bid-ask bounces

One could do daily and add lagged returns as a way to deal with this

import wrds
import psycopg2 
from codesnippets import get_returns
conn=wrds.Connection()

def get_returns(tickers,conn,startdate,enddate,variable='ret'):
    ticker=tickers[0]
    df = conn.raw_sql("""
                          select a.permno, b.ncusip, b.ticker, a.date, b.shrcd,
                          a.ret, a.vol, a.shrout, a.prc, a.cfacpr, a.cfacshr,a.retx
                          from crsp.msf as a
                          left join crsp.msenames as b
                          on a.permno=b.permno
                          and b.namedt<=a.date
                          and a.date<=b.nameendt
                          where a.date between '"""+ startdate+"""'  and '"""+ enddate+            
                          """' and  b.ticker='"""+ticker+"'")
    # and b.shrcd between 10 and 11
    # and b.exchcd between 1 and 3
            
    df.set_index(['date','permno'],inplace=True)
    df=df[variable].unstack()
    return df

Enter your WRDS username [Alan.Moreira]: moreira5
Enter your password: ···········

WRDS recommends setting up a .pgpass file.
You can find more info here:
https://www.postgresql.org/docs/9.5/static/libpq-pgpass.html.
Loading library list...
Done

df=get_returns(['BRK'],conn,'1/1/1960','1/1/2022',variable='prc')
df.abs().plot()

<AxesSubplot:xlabel='date'>
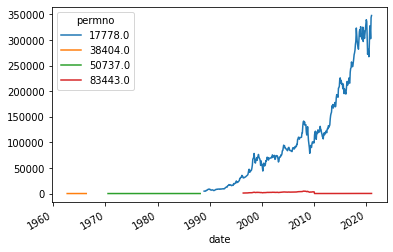
../../_images/MultiFactorModels_7_1.png

Berkshire seems to have multiple securities issue over time

We will simply use the blue series which matches wha tI see in google, but you could think about piecing toghether the blue and the green to expand the sample. But one would have to read in detail to see what happened and if that really makes sense

df=get_returns(['BRK'],conn,'1/1/1960','1/1/2022',variable='ret')
(df[17778.0]+1).cumprod().plot()

<AxesSubplot:xlabel='date'>
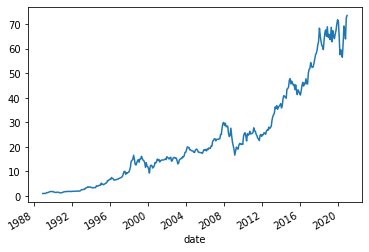
../../_images/MultiFactorModels_9_1.png

Lets now merge with the factors

Firs note that they are both monthy bu the factors index is period type while the Berkshire index is date time

dff6.index

PeriodIndex(['1963-07', '1963-08', '1963-09', '1963-10', '1963-11', '1963-12',
             '1964-01', '1964-02', '1964-03', '1964-04',
             ...
             '2020-06', '2020-07', '2020-08', '2020-09', '2020-10', '2020-11',
             '2020-12', '2021-01', '2021-02', '2021-03'],
            dtype='period[M]', name='Date', length=693, freq='M')

df.index

DatetimeIndex(['1962-08-31', '1962-09-28', '1962-10-31', '1962-11-30',
               '1962-12-31', '1963-01-31', '1963-02-28', '1963-03-29',
               '1963-04-30', '1963-05-31',
               ...
               '2020-03-31', '2020-04-30', '2020-05-29', '2020-06-30',
               '2020-07-31', '2020-08-31', '2020-09-30', '2020-10-30',
               '2020-11-30', '2020-12-31'],
              dtype='datetime64[ns]', name='date', length=644, freq=None)

We can deal with this by converting either the df dataframe to period or the dff6 dataframe to datetime

df[17778.0].to_period("M").tail()

date
2020-08    0.115550
2020-09   -0.023077
2020-10   -0.054690
2020-11    0.136159
2020-12    0.012008
Freq: M, Name: 17778.0, dtype: float64

dff6.to_timestamp('M').tail()
Mkt-RF SMB HML RMW CMA RF Mom
Date
2020-11-30 12.47 6.75 2.11 -2.78 1.05 0.01 -12.25
2020-12-31 4.63 4.67 -1.36 -2.15 0.00 0.01 -2.42
2021-01-31 -0.03 6.88 2.85 -3.33 4.68 0.00 4.37
2021-02-28 2.78 4.51 7.08 0.09 -1.97 0.00 -7.68
2021-03-31 3.09 -0.98 7.40 6.43 3.44 0.00 -5.83

Here I will use the first method

df=(dff6/100).merge(df[17778.0].to_period("M"),left_index=True,right_index=True,how='inner').dropna(how='any')
df.rename(columns={17778:'BRK'},inplace=True)
df
Mkt-RF SMB HML RMW CMA RF Mom BRK
1988-11 -0.0229 -0.0166 0.0130 -0.0028 0.0160 0.0057 0.0042 -0.005291
1988-12 0.0149 0.0201 -0.0154 0.0063 -0.0037 0.0063 0.0042 0.000000
1989-01 0.0610 -0.0223 0.0049 -0.0103 0.0016 0.0055 -0.0014 0.047872
1989-02 -0.0225 0.0267 0.0090 -0.0081 0.0190 0.0061 0.0094 -0.040609
1989-03 0.0157 0.0077 0.0047 0.0000 0.0079 0.0067 0.0356 0.047619
... ... ... ... ... ... ... ... ...
2020-08 0.0763 -0.0094 -0.0294 0.0427 -0.0144 0.0001 0.0051 0.115550
2020-09 -0.0363 0.0007 -0.0251 -0.0115 -0.0177 0.0001 0.0305 -0.023077
2020-10 -0.0210 0.0476 0.0403 -0.0060 -0.0053 0.0001 -0.0303 -0.054690
2020-11 0.1247 0.0675 0.0211 -0.0278 0.0105 0.0001 -0.1225 0.136159
2020-12 0.0463 0.0467 -0.0136 -0.0215 0.0000 0.0001 -0.0242 0.012008

386 rows × 8 columns

df.BRK=df.BRK-df.RF

Start with the CAPM

import statsmodels.api as sm
temp=df.copy() 
x= sm.add_constant(temp['Mkt-RF'])
y= temp['BRK']
results= sm.OLS(y,x).fit()
results.summary()
OLS Regression Results
Dep. Variable: BRK R-squared: 0.212
Model: OLS Adj. R-squared: 0.210
Method: Least Squares F-statistic: 103.6
Date: Tue, 04 May 2021 Prob (F-statistic): 1.06e-21
Time: 09:25:48 Log-Likelihood: 592.00
No. Observations: 386 AIC: -1180.
Df Residuals: 384 BIC: -1172.
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 0.0060 0.003 2.210 0.028 0.001 0.011
Mkt-RF 0.6236 0.061 10.178 0.000 0.503 0.744
Omnibus: 83.751 Durbin-Watson: 2.060
Prob(Omnibus): 0.000 Jarque-Bera (JB): 261.498
Skew: 0.974 Prob(JB): 1.65e-57
Kurtosis: 6.530 Cond. No. 23.0


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
results.params[0]*12

0.07164885662375453

Market beta of about 0.6 and alpha of 7% per year!

Six factor model

temp=df.copy() 
x= sm.add_constant(temp.drop(['BRK','RF'],axis=1))
y= temp['BRK']
results= sm.OLS(y,x).fit()
results.summary()
OLS Regression Results
Dep. Variable: BRK R-squared: 0.348
Model: OLS Adj. R-squared: 0.338
Method: Least Squares F-statistic: 33.74
Date: Tue, 04 May 2021 Prob (F-statistic): 1.35e-32
Time: 09:26:02 Log-Likelihood: 628.50
No. Observations: 386 AIC: -1243.
Df Residuals: 379 BIC: -1215.
Df Model: 6
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 0.0046 0.003 1.774 0.077 -0.001 0.010
Mkt-RF 0.7599 0.067 11.357 0.000 0.628 0.892
SMB -0.3946 0.091 -4.316 0.000 -0.574 -0.215
HML 0.4836 0.118 4.091 0.000 0.251 0.716
RMW 0.2687 0.121 2.214 0.027 0.030 0.507
CMA -0.1286 0.172 -0.749 0.454 -0.466 0.209
Mom -0.0077 0.057 -0.135 0.892 -0.119 0.104
Omnibus: 89.527 Durbin-Watson: 2.143
Prob(Omnibus): 0.000 Jarque-Bera (JB): 237.376
Skew: 1.105 Prob(JB): 2.85e-52
Kurtosis: 6.143 Cond. No. 80.7


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print(results.params[0]*12)

0.055415983696528254

  • What do we learn about Warren Investment style?

  • What do we learn about Warren specific stock picking skills?

Aplication 2: Does Cathie Wood has some secret sauce? Performance evalaution of ARKK

df=get_returns(['ARKK'],conn,'1/1/1960','1/1/2022',variable='ret')
(df+1).cumprod().plot()

<AxesSubplot:xlabel='date'>
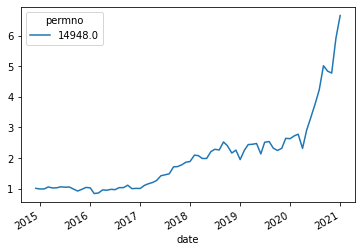
../../_images/MultiFactorModels_27_1.png 
df=(dff6/100).merge(df.to_period("M"),left_index=True,right_index=True,how='inner').dropna(how='any')
df.rename(columns={14948.0:'ARKK'},inplace=True)
df.ARKK=df.ARKK-df.RF

temp=df.copy() 
x= sm.add_constant(temp['Mkt-RF'])
y= temp['ARKK']
results= sm.OLS(y,x).fit()
results.summary()
OLS Regression Results
Dep. Variable: ARKK R-squared: 0.691
Model: OLS Adj. R-squared: 0.687
Method: Least Squares F-statistic: 160.9
Date: Tue, 04 May 2021 Prob (F-statistic): 4.98e-20
Time: 09:28:12 Log-Likelihood: 120.93
No. Observations: 74 AIC: -237.9
Df Residuals: 72 BIC: -233.2
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 0.0115 0.006 2.016 0.048 0.000 0.023
Mkt-RF 1.5768 0.124 12.684 0.000 1.329 1.825
Omnibus: 4.334 Durbin-Watson: 1.974
Prob(Omnibus): 0.115 Jarque-Bera (JB): 3.484
Skew: 0.465 Prob(JB): 0.175
Kurtosis: 3.516 Cond. No. 22.3


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print(results.params[0]*12)

0.1385421007873513

temp=df.copy() 
x= sm.add_constant(temp.drop(['ARKK','RF'],axis=1))
y= temp['ARKK']
results= sm.OLS(y,x).fit()
results.summary()
OLS Regression Results
Dep. Variable: ARKK R-squared: 0.818
Model: OLS Adj. R-squared: 0.802
Method: Least Squares F-statistic: 50.21
Date: Tue, 04 May 2021 Prob (F-statistic): 6.69e-23
Time: 09:28:44 Log-Likelihood: 140.55
No. Observations: 74 AIC: -267.1
Df Residuals: 67 BIC: -251.0
Df Model: 6
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 0.0059 0.005 1.234 0.221 -0.004 0.015
Mkt-RF 1.3860 0.126 11.009 0.000 1.135 1.637
SMB 0.5065 0.210 2.410 0.019 0.087 0.926
HML -0.8120 0.200 -4.067 0.000 -1.211 -0.413
RMW -0.1642 0.326 -0.504 0.616 -0.815 0.487
CMA -0.9219 0.351 -2.624 0.011 -1.623 -0.221
Mom -0.2654 0.152 -1.747 0.085 -0.569 0.038
Omnibus: 10.376 Durbin-Watson: 2.119
Prob(Omnibus): 0.006 Jarque-Bera (JB): 10.331
Skew: 0.806 Prob(JB): 0.00571
Kurtosis: 3.866 Cond. No. 83.6


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print(results.params[0]*12)

0.0704257048781867

  • What do we learn about Cathie Wood investment style?

  • What do we learn about Cathie Wook investment skills?

  • How do you think about the R-squared? Is a large Rsquared good or bad in this case?

Application 3: what is a good Momentum ETF?

names=['VFMO','QMOM','FDMO','MTUM','IMTM','IMOM']
dmom=get_returns([names[0]],conn,'1/1/1960','1/1/2022')
for n in names[1:]:
    df=get_returns([n],conn,'1/1/1960','1/1/2022')
    dmom=dmom.merge(df,left_index=True,right_index=True,how='outer')
dmom.columns=names    
(dmom+1).cumprod().plot()

<AxesSubplot:xlabel='date'>
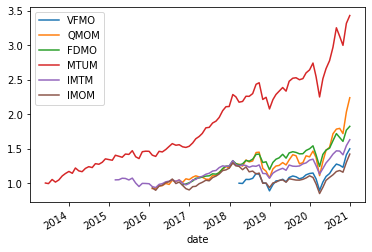
../../_images/MultiFactorModels_35_1.png 
# lets merge
df=(dff6/100).merge(dmom.to_period("M"),left_index=True,right_index=True,how='inner')
# lets conver to excess returns
df[names]=df[names].subtract(df['RF'],axis=0)

temp.columns

Index(['Mkt-RF', 'SMB', 'HML', 'RMW', 'CMA', 'RF', 'Mom   ', 'VFMO', 'QMOM',
       'FDMO', 'MTUM', 'IMTM', 'IMOM'],
      dtype='object')

temp=df.copy() 
x= sm.add_constant(temp[['Mkt-RF','Mom   ']])
results=pd.DataFrame([],index=[],columns=names)
for n in names:
    y= temp[n]
    res= sm.OLS(y,x,missing='drop').fit()
    results.at['alpha',n]=res.params[0]
    results.at['t(alpha)',n]=res.tvalues[0]
    results.at['betamkt',n]=res.params[1]
    results.at['t(betamkt)',n]=res.tvalues[1]
    results.at['betamom',n]=res.params[2]
    results.at['t(betamom)',n]=res.tvalues[2]
    results.at['R-squared',n]=res.rsquared
    results.at['indio risk',n]=res.resid.std()*12**0.5
    results.at['sample size',n]=res.nobs
results
VFMO QMOM FDMO MTUM IMTM IMOM
alpha -0.001458 -0.002718 -0.002354 0.001112 -0.002008 -0.005894
t(alpha) -0.430959 -0.63581 -1.664363 0.869311 -0.847557 -1.459713
betamkt 1.132283 1.39176 1.024135 1.00483 0.761741 0.958616
t(betamkt) 16.762846 13.753471 31.996319 31.597999 13.558808 10.029335
betamom 0.186237 0.394746 0.254752 0.345416 0.09699 0.15187
t(betamom) 2.178768 3.281823 6.461063 9.626601 1.568105 1.336749
R-squared 0.917845 0.782982 0.960205 0.919332 0.756383 0.674357
indio risk 0.064076 0.107838 0.032342 0.039782 0.065174 0.101857
sample size 34.0 60.0 51.0 92.0 71.0 60.0

  • what do you conclude?

  • Which ETF would you pick?

  • How to think about the alpha here?

  • How do you think about the R-squared? Is a large Rsquared good or bad in this case?

  • How do you account for the differnece in market betas when investing?