Show code cell content

Hide code cell content

#!pip install wrds
import psycopg2 
import wrds
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

import pandas_datareader.data as web

def get_factors(factors='CAPM',freq='daily'):   
    
    if freq=='monthly':
        freq_label=''
    else:
        freq_label='_'+freq


    if factors=='CAPM':
        fama_french = web.DataReader("F-F_Research_Data_Factors"+freq_label, "famafrench",start="1921-01-01")
        daily_data = fama_french[0]
    
     
        df_factor = daily_data[['RF','Mkt-RF']] 
    elif factors=='FF3':
        fama_french = web.DataReader("F-F_Research_Data_Factors"+freq_label, "famafrench",start="1921-01-01")
        daily_data = fama_french[0]

        df_factor = daily_data[['RF','Mkt-RF','SMB','HML']]
    elif factors=='FF5':

        fama_french = web.DataReader("F-F_Research_Data_Factors"+freq_label, "famafrench",start="1921-01-01")
        daily_data = fama_french[0]

        df_factor = daily_data[['RF','Mkt-RF','SMB','HML']]
        fama_french2 = web.DataReader("F-F_Research_Data_5_Factors_2x3"+freq_label, "famafrench",start="1921-01-01")
        daily_data2 = fama_french2[0]

        df_factor2 = daily_data2[['RMW','CMA']]
        df_factor=df_factor.merge(df_factor2,on='Date',how='outer')    
        
    else:
        fama_french = web.DataReader("F-F_Research_Data_Factors"+freq_label, "famafrench",start="1921-01-01")
        daily_data = fama_french[0]

        df_factor = daily_data[['RF','Mkt-RF','SMB','HML']]
        fama_french2 = web.DataReader("F-F_Research_Data_5_Factors_2x3"+freq_label, "famafrench",start="1921-01-01")
        daily_data2 = fama_french2[0]

        df_factor2 = daily_data2[['RMW','CMA']]
        df_factor=df_factor.merge(df_factor2,on='Date',how='outer')   
        fama_french = web.DataReader("F-F_Momentum_Factor"+freq_label, "famafrench",start="1921-01-01")
        df_factor=df_factor.merge(fama_french[0],on='Date')
        df_factor.columns=['RF','Mkt-RF','SMB','HML','RMW','CMA','MOM']    
    if freq=='monthly':
        df_factor.index = pd.to_datetime(df_factor.index.to_timestamp())
    else:
        df_factor.index = pd.to_datetime(df_factor.index)
        


    return df_factor/100

11. Cross-Sectional Trading strategies

---

🎯 Learning Objectives

1. Contrast timing vs. cross-sectional approaches
   Recognize that characteristic-based strategies keep aggregate market exposure roughly constant and instead shift weight across individual stocks according to firm-level signals.

2. Master the four-step portfolio recipe
   Build a signal → sort stocks each month → weight within buckets (equal or market-cap) → form the long-short spread (top – bottom), always using information that is known on the trade date.

3. Construct the market-cap-weighted benchmark correctly
   Compute market capitalizations from lagged price × shares-outstanding and show how to aggregate them to the total-market portfolio, avoiding look-ahead bias.

4. Organize large equity data sets efficiently
   Work with “stacked” (date-firm) data frames, merge CRSP returns with characteristics, and reshape the grouped returns so they are ready for analysis and plotting.

5. Code a reusable function that maps any signal to portfolios
   Generalize the recipe into a single function that takes a signal (X), number of groups, and weighting choice, and then delivers decile returns, cumulative-return plots, and the long-short series.

6. Develop empirical intuition about trade-offs
   Explore how the number of groups, the dispersion of the signal, and the choice of weights influence the return spread, volatility, and diversification of the resulting portfolios.

---

11.1. The Market-Cap Weighted strategy

As a warm up for you first factor construction we will construct the returns on the market portfolio

• In some way that is the most important strategy ever

• It completely revolutionized Wall Street leading to the rise of index funds

How to do it?

• start with a vector of market capitalization for all relevant assets \(M_t=[m_t^{AAPL},m_t^{GOOG},m_t^{TSLA},..]\)

\[m_t^{AAPL}=P^{AAPL}_t\times SharesOutstanding^{AAPL}\]

The strategy then set the weights simply to

\[X_t=\frac{M_t}{\sum_i^Im^i_t}\]

So at end of month t you look at the market caps, construct the weights, and buy the assets with weights \(X_t\) (at prices \(P_t\)) to earn

\[R^{mcap}_{t+1}=X_tR_{t+1}\]

at the end of the next month.

That is you pay \(P_t\) and get back \(P_{t+1}+D_{t+1}\), hence return \(R_{t+1}=\frac{P_{t+1}+D_{t+1}}{P_t}\)

This portfolio has nice properties

1. This portfolio is very easy to trade. It does not require re-balancing as your weights naturally go up if the stock rallies and go down if the stock crashes

2. You can implement this approach to any subset of firms (for example SP500 or Russel2000) are market cap indexes that track a particular universe of stocks and we will be using it in our characteristic-based portfolios shortly

3. By buying proportionally to market cap you never have to build a huge position in a tiny stock–so this is much easier to trade!

   • Equal weighted portfolio tend to be very hard to trade and the alphas that you get there are mostly a mirrage, unless you focus on large caps

Steps

1. Get firm level monthly return data with market capitalizations

2. clean up/organize the data set

3. Make sure to lag the market cap signal so that we use prices from last month to trade at the start of this month ( we could also skip another month to be extra sure)

4. Construct the weighted average of returns across stocks for each date

11.1.1. Stacked Datasets

• We will now work with large data sets

• Data sets that include all US stocks

• Because there are many stocks, we have to work with it stacked

Organizing the data

The objective here is to have a data set with

• Security identifier

• Date of the information

• Monthly return of the firm in that month

• Market capitalization of the firm in that month

conn=wrds.Connection() 

WRDS recommends setting up a .pgpass file.
Created .pgpass file successfully.
You can create this file yourself at any time with the create_pgpass_file() function.
Loading library list...
Done

import datetime as dt

from dateutil.relativedelta import *
from pandas.tseries.offsets import *

###################



crsp = conn.raw_sql("""
                      select a.permno,a.permco, a.date, b.shrcd, b.exchcd,b.ticker,
                      a.ret, a.shrout, a.prc,a.retx
                      from crsp.msf as a
                      left join crsp.msenames as b
                      on a.permno=b.permno
                      and b.namedt<=a.date
                      and a.date<=b.nameendt
                      where a.date between '01/31/2015' and '12/31/2024'
                      and b.exchcd between 1 and 3
                      and b.shrcd between 10 and 11
                      """, date_cols=['date']) 


# this saves it
crsp.to_pickle('../../assets/data/crspm.pkl')
# variables downloaded

# 1. Permno-- are unique indentifier to a security 
# (for exmaple a stock that has multiple types of stocks will have multiple permnos)

# 2. shrco is the type of share: common share, ADR, ETF, ....
# we will focus on common shares

# 3. exchcd is the code of the exchange where the stock was originally listed
# we will focus on stock listed in the 3 major stock exchanges ( basically the whole market)

# 4. ret,retx, shrout,  prc, are the stock return, the stock return excluding dividends, number of shares outstanding, and price

# 5. date is the trading date of the return

---

If you don’t want to deal with that you can simply get the data by running the code below

crsp=pd.read_pickle('https://github.com/amoreira2/Fin418/blob/main/assets/data/crspm20022016.pkl?raw=true')

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[1], line 1
----> 1 crsp=pd.read_pickle('https://github.com/amoreira2/Fin418/blob/main/assets/data/crspm20022016.pkl?raw=true')

NameError: name 'pd' is not defined

crsp=crsp[['permco','permno','ticker','date','ret','shrout','prc']].copy()
# change variable format to int
crsp[['permno']]=crsp[['permno']].astype(int)

# Line up date to be end of month 
crsp['date']=crsp['date']+pd.offsets.MonthEnd(0)

# calculate market equity
# why do we use absolute value of price?
crsp['me']=crsp['prc'].abs()*crsp['shrout'] 

# sort by permno and date and also drop duplicates
crsp=crsp.sort_values(by=['permno','date']).drop_duplicates()

crsp

	permco	permno	ticker	date	ret	shrout	prc	me
60	7953	10001	EGAS	2015-02-28	0.035898	10488.0	10.10	105928.80
61	7953	10001	EGAS	2015-03-31	-0.000495	10452.0	9.96	104101.92
62	7953	10001	EGAS	2015-04-30	0.011044	10452.0	10.07	105251.64
63	7953	10001	EGAS	2015-05-31	-0.006951	10488.0	10.00	104880.00
64	7953	10001	EGAS	2015-06-30	0.030000	10493.0	10.30	108077.90

from pandas.tseries.offsets import *
crsp=crsp[['permco','permno','ticker','date','ret','shrout','prc']].copy()
# change variable format to int
crsp[['permno']]=crsp[['permno']].astype(int)
crsp[['permco']]=crsp[['permco']].astype(int)
# Line up date to be end of month 
crsp['date']=crsp['date']+MonthEnd(0)

# calculate market equity
# why do we use absolute value of price?
crsp['me']=crsp['prc'].abs()*crsp['shrout'] 
# drop price and shareoustandng since we won't need it anymore
crsp=crsp.drop(['prc','shrout'], axis=1)
crsp_me=crsp.groupby(['date','permco'])['me'].sum().reset_index()


# largest mktcap within a permco/date
crsp_maxme = crsp.groupby(['date','permco'])['me'].max().reset_index()

# join by jdate/maxme to find the permno
crsp=pd.merge(crsp, crsp_maxme, how='inner', on=['date','permco','me'])

# drop me column and replace with the sum me
crsp=crsp.drop(['me'], axis=1)

# join with sum of me to get the correct market cap info
crsp=pd.merge(crsp, crsp_me, how='inner', on=['date','permco'])

# sort by permno and date and also drop duplicates
crsp=crsp.sort_values(by=['permno','date']).drop_duplicates()

crsp.head()

	permco	permno	ticker	date	ret	me
550	7953	10001	EWST	2002-01-31	-0.013100	28995.8000
551	7953	10001	EWST	2002-02-28	-0.053097	27488.3000
552	7953	10001	EWST	2002-03-31	-0.015888	26738.4000
553	7953	10001	EWST	2002-04-30	-0.043269	25581.4500
554	7953	10001	EWST	2002-05-31	0.014824	25960.6725

Take time to note the stacked structure of the data set

• Before with a “rectangular” data set we need two coordinates, row and column, to identify the return of an asset in a particular date

• It was easier to manipulate but we would need one dataframe for each different firm variable: In this case one for return and one for market equity

• As we work with many signals, this becomes intractable because we would need many dataframes

• As we work with many asset, this would become intractable because we would need dataframes with many columns with most locations empty. This is very inefficient and hard to manipulate

Stacked data sets

• Now we need two coordinates both in columns, “date” and “permco”, to identify one firm-date observation, and then a third coordinate, the column names to identify the particular variable for that firm-date pair

Lagging the market cap signal

• We use the method .shift(d) which “lags” the data by d periods.

• It is important that we have our data set sorted by date

• shift(d) simply shifts the rows. So you have to make sure that it is actually lagging by date.

The way to do that is to groupby security and applying the shift within security.

Why this is important?

• Because the data set is stacked so when you shift the first month of security n, it will end up returning the last month of security n-1.

• By “grouping by” we correctly assign a missing value there since we don’t have the data

# sort by permno and date and set as index
crsp=crsp.sort_values(by=['permno','date'])
crsp['me_l1']=crsp.me.shift(1)

crsp

	permco	permno	ticker	date	ret	shrout	prc	me	me_l1
60	7953	10001	EGAS	2015-02-28	0.035898	10488.0	10.10000	1.059288e+05	NaN
61	7953	10001	EGAS	2015-03-31	-0.000495	10452.0	9.96000	1.041019e+05	1.059288e+05
62	7953	10001	EGAS	2015-04-30	0.011044	10452.0	10.07000	1.052516e+05	1.041019e+05
63	7953	10001	EGAS	2015-05-31	-0.006951	10488.0	10.00000	1.048800e+05	1.052516e+05
64	7953	10001	EGAS	2015-06-30	0.030000	10493.0	10.30000	1.080779e+05	1.048800e+05
...	...	...	...	...	...	...	...	...	...
456021	53453	93436	TSLA	2024-08-31	-0.077391	3194640.0	214.11000	6.840044e+08	7.413801e+08
456022	53453	93436	TSLA	2024-09-30	0.221942	3207000.0	261.63000	8.390474e+08	6.840044e+08
456023	53453	93436	TSLA	2024-10-31	-0.045025	3210060.0	249.85001	8.020335e+08	8.390474e+08
456024	53453	93436	TSLA	2024-11-30	0.381469	3210060.0	345.16000	1.107984e+09	8.020335e+08
456025	53453	93436	TSLA	2024-12-31	0.170008	3210060.0	403.84000	1.296351e+09	1.107984e+09

457062 rows × 9 columns

crsp.iloc[20:40]

	permco	permno	ticker	date	ret	shrout	prc	me	me_l1
302	7953	10001	EGAS	2016-10-31	0.619948	10520.0	12.350	129922.00	80657.72
303	7953	10001	EGAS	2016-11-30	0.012146	10520.0	12.500	131500.00	129922.00
304	7953	10001	EGAS	2016-12-31	0.010000	10520.0	12.550	132026.00	131500.00
305	7953	10001	EGAS	2017-01-31	0.007968	10520.0	12.650	133078.00	132026.00
306	7953	10001	EGAS	2017-02-28	0.000000	10520.0	12.650	133078.00	133078.00
307	7953	10001	EGAS	2017-03-31	0.009881	10520.0	12.700	133604.00	133078.00
308	7953	10001	EGAS	2017-04-30	-0.015748	10520.0	12.500	131500.00	133604.00
309	7953	10001	EGAS	2017-05-31	0.016000	10520.0	12.700	133604.00	131500.00
310	7953	10001	EGAS	2017-06-30	0.023622	10520.0	12.925	135971.00	133604.00
311	7953	10001	EGAS	2017-07-31	0.001934	10520.0	12.950	136234.00	135971.00
1010	7975	10025	AEPI	2015-02-28	0.010976	5083.0	50.660	257504.78	136234.00
1011	7975	10025	AEPI	2015-03-31	0.086459	5083.0	55.040	279768.32	257504.78
1012	7975	10025	AEPI	2015-04-30	-0.089753	5103.0	50.100	255660.30	279768.32
1013	7975	10025	AEPI	2015-05-31	-0.001397	5103.0	50.030	255303.09	255660.30
1014	7975	10025	AEPI	2015-06-30	0.103338	5103.0	55.200	281685.60	255303.09
1015	7975	10025	AEPI	2015-07-31	-0.124094	5103.0	48.350	246730.05	281685.60
1016	7975	10025	AEPI	2015-08-31	0.126163	5103.0	54.450	277858.35	246730.05
1017	7975	10025	AEPI	2015-09-30	0.052893	5103.0	57.330	292554.99	277858.35
1018	7975	10025	AEPI	2015-10-31	0.395430	5103.0	80.000	408240.00	292554.99
1019	7975	10025	AEPI	2015-11-30	0.139750	5103.0	91.180	465291.54	408240.00

crsp['me_l1']=crsp.groupby(['permno']).me.shift(1)
change_idx = crsp['ticker'].ne(crsp['ticker'].shift()).idxmax()
crsp.iloc[20:40]
# did it get fixed?

	permco	permno	ticker	date	ret	shrout	prc	me	me_l1
1030	7975	10025	AEPI	2016-10-31	0.003932	5114.0	109.55	560238.70	559318.18
1031	7975	10025	AEPI	2016-11-30	0.075764	5114.0	117.85	602684.90	560238.70
1032	7975	10025	AEPI	2016-12-31	-0.014849	5114.0	116.10	593735.40	602684.90
756	7976	10026	JJSF	2015-02-28	0.031288	18688.0	101.19	1891038.72	NaN
757	7976	10026	JJSF	2015-03-31	0.058010	18689.0	106.70	1994116.30	1891038.72
758	7976	10026	JJSF	2015-04-30	-0.022212	18691.0	104.33	1950032.03	1994116.30
759	7976	10026	JJSF	2015-05-31	0.033260	18691.0	107.80	2014889.80	1950032.03
760	7976	10026	JJSF	2015-06-30	0.029963	18692.0	110.67	2068643.64	2014889.80
761	7976	10026	JJSF	2015-07-31	0.069486	18699.0	118.36	2213213.64	2068643.64
762	7976	10026	JJSF	2015-08-31	-0.037175	18699.0	113.96	2130938.04	2213213.64
763	7976	10026	JJSF	2015-09-30	0.000527	18676.0	113.66	2122714.16	2130938.04
764	7976	10026	JJSF	2015-10-31	0.080327	18676.0	122.79	2293226.04	2122714.16
765	7976	10026	JJSF	2015-11-30	-0.049760	18686.0	116.68	2180282.48	2293226.04
766	7976	10026	JJSF	2015-12-31	0.003257	18677.0	116.67	2179045.59	2180282.48
767	7976	10026	JJSF	2016-01-31	-0.074484	18686.0	107.98	2017714.28	2179045.59
768	7976	10026	JJSF	2016-02-29	0.026023	18686.0	110.79	2070221.94	2017714.28
769	7976	10026	JJSF	2016-03-31	-0.019135	18617.0	108.28	2015848.76	2070221.94
770	7976	10026	JJSF	2016-04-30	-0.066033	18619.0	101.13	1882939.47	2015848.76
771	7976	10026	JJSF	2016-05-31	0.043212	18619.0	105.50	1964304.50	1882939.47
772	7976	10026	JJSF	2016-06-30	0.134218	18618.0	119.27	2220568.86	1964304.50

Rmkt=crsp.groupby(['date']).apply(lambda x:(x.ret*(x.me_l1/x.me_l1.sum())).sum(),include_groups=False)

• The groupby(['date']) method groups the data by month so we obtain the return of the portfolio in that month

• (x.me/x.me.sum()) has the weights in a given date, which for each date will return a vector that adds up to one.

• (x.ret*(x.me/x.me.sum()) multiplies the return of each asset by the weight

• (x.ret*(x.me/x.me.sum())).sum() sum all up to get the reutrn of the portfolio

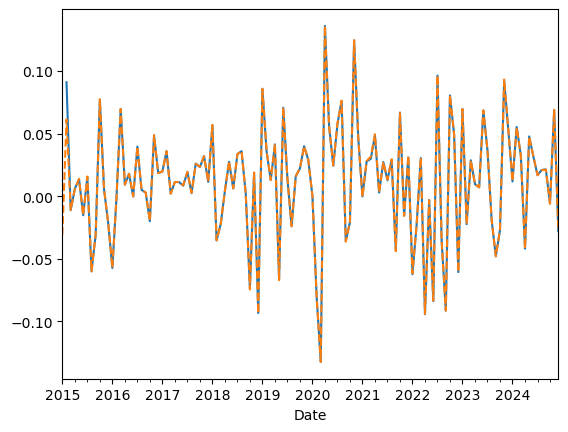
Lets compare our factor with the one ken french website

#Lets look at the cumulative return
df=get_factors('CAPM',freq='monthly')

(Rmkt).plot()
(df['Mkt-RF']+df['RF'])['2015':'2024'].plot(linestyle='dashed')

c:\Users\alan.moreira\Anaconda3\lib\site-packages\pandas_datareader\famafrench.py:114: FutureWarning: The argument 'date_parser' is deprecated and will be removed in a future version. Please use 'date_format' instead, or read your data in as 'object' dtype and then call 'to_datetime'.
  df = read_csv(StringIO("Date" + src[start:]), **params)
c:\Users\alan.moreira\Anaconda3\lib\site-packages\pandas_datareader\famafrench.py:114: FutureWarning: The argument 'date_parser' is deprecated and will be removed in a future version. Please use 'date_format' instead, or read your data in as 'object' dtype and then call 'to_datetime'.
  df = read_csv(StringIO("Date" + src[start:]), **params)

<Axes: xlabel='Date'>

Things to try

• Suppose you wanted to construct something “like” the SP500? I.e. do market cap weights but only for the 500 largest firms in a given month. How would you do that?

• Suppose you lag market cap 2 months instead of 1 does it make any difference? Do you expect there is any difference

• Suppose you drop the stocks with “negative” prices, does it make a difference?

11.2. Characteristic-Based Strategies

• So far we have looked at strategies that go in and out of a particular asset according to a signal.

• Now we will look at strategies that trade of asset characteristics

The recipe

1. Construct a characteristic for each stock.

   • It can be based on accounting data (aka fundamentals), return data, textual data from earning calls, twitter activity, ownership, shorting activity, satellite images–

   • You can do for anything

   • What is important is that for each stock in each date you have a value for this characteristic

   • And you have a sense/theory of how this chracteristic relates to expected returns

2. On a given date sort stocks by this characteristic.

   • It is key that this characteristic is in fact known at sorting date!

   • Extremely careful not to introduce “look-ahead” bias

3. Construct portfolios by dividing stocks in deciles/quintiles and “10” form portfolios of stocks that have similar characteristic

   • You can either equal weight or value weight within portfolio

   • Value-weighed portfolios are easier to trade, but if you are focused on large caps, you can go with either

   • But what is important is that each portfolio will have stocks of have very different characteristic values

4. Construct the long-short where you go long portfolio “10” and short portfolio “1” (or vice versa) but the point is to take a bet on the characteristic spread

The goal here is to produce alpha

• this is a simple and algorithimic way to implement your idea in a way that harvest the benefits of diversification

• Instead of betting on Apple because it is exposed to tariffs, build a tariff exposure “characteristic”

From “names” to characteristics

• The sorting by date keeps the stocks inside the portfolios with similar characteristics

• This sorting will “work” if these chracteristics are good proxies for the behavior of the stock returns

• Indeed, the key is that each portfolio has stocks of vastly different characterisitcs and keeps churning as firms change

  • Let’s take MSFT (microsoft) as an example:

  • MSFT transitioned from being small in the 80’s to be gigantic in the 90’s, as a result, it moved up from the small portfolio to the big portfolio

  • During the Tech boom when MSFT had a huge valuation relative to it’s book value, it went to the low BM portfolio

  • But then MSFT transtioned back to the high BM portfolio once it’s market valuation collapsed in the aftermath of the techbubble

  • Now with AI, MSFT is back into the low BM portfolio

  • During these 80 years MSFT changed dramatically and the characteristic changed with it…

• The key is that firms’ characteristics change over time, by constructing portfolios, we hope to estimate some stable parameters (for example, alpha and beta)

• But it doesn’t work always, if you use the first letter of stock ticker to construct 26 portfolios you are unlikely to get spread in average returns and most likely each portfolio will resemble the market portfolio but with much more volatility.

• The characteristics have to capture the right economics/market dynamics

11.2.1. Example: Value investing

Wall street talks a lot in terms of earnings

11.2.2. Implementing the recipe

1. We will start with a constructed characteristic \(c_{i,t}\)

2. Produce 10 portfolios based on this characteristic

   • Members of portfolio 1 in date t have the bottom 10% value of the characteristics in date t

   • Members of portfolio 2 in date t have characteristic between 10% and 20% of the characteristics in date t

3. Given these memberships for each date we will the construct return by buying at the closing price of date t and selling at the closing on date t+1

   • We will typically work with monthly data, so this should read as the closing of the last date of months t and t+1

We start by loading a dataset where you have many signals

11.2.2.1. Our Characteristic data

url = "https://github.com/amoreira2/Fin418/blob/main/assets/data/characteristics20022016.pkl?raw=true"

df_X = pd.read_pickle(url)
df_X=df_X.reset_index()
df_X.date=df_X.date+pd.tseries.offsets.MonthEnd()
df_X.describe()

	date	permno	re	rf	rme	size	value	prof	fscore	debtiss	...	momrev	valuem	nissm	strev	ivol	betaarb	indrrev	price	age	shvol
count	163913	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	...	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000	163913.000000
mean	2009-07-17 14:37:46.612166400	60452.050222	0.007979	0.001032	0.005875	15.550336	-0.912667	-1.556057	4.933819	0.362827	...	0.057370	-0.948673	0.700911	0.014663	0.015696	1.032455	0.006188	3.664508	5.512095	1.057609
min	2002-01-31 00:00:00	10026.000000	-0.870345	0.000000	-0.172300	11.501877	-8.756389	-10.213809	0.000000	0.000000	...	-3.055986	-8.818536	0.329881	-0.868645	0.000463	0.241380	-0.820129	0.570980	3.637586	0.003904
25%	2005-10-31 00:00:00	35238.000000	-0.040199	0.000000	-0.018300	14.676361	-1.351522	-2.087953	4.000000	0.000000	...	-0.053707	-1.384280	0.682923	-0.035392	0.009952	0.851590	-0.033465	3.258097	5.003946	0.748381
50%	2009-06-30 00:00:00	73139.000000	0.008931	0.000200	0.009200	15.293713	-0.850813	-1.346370	5.000000	0.000000	...	0.072849	-0.900369	0.694412	0.013158	0.013612	1.003569	0.002659	3.679082	5.575949	0.999129
75%	2013-03-31 00:00:00	84168.000000	0.056648	0.001500	0.032300	16.240260	-0.378992	-0.875085	6.000000	1.000000	...	0.191116	-0.417606	0.701702	0.061674	0.019028	1.178665	0.040915	4.063370	6.165418	1.312665
max	2016-12-31 00:00:00	93436.000000	1.597907	0.004400	0.113500	20.388632	2.370495	0.837982	8.000000	1.000000	...	3.302411	2.329125	2.711109	2.596567	0.218682	2.350102	2.134880	11.631769	6.555357	4.319359
std	NaN	27258.977322	0.094412	0.001368	0.041751	1.161036	0.782885	0.965714	1.290275	0.480817	...	0.259801	0.784227	0.060812	0.095684	0.008647	0.251549	0.077490	0.685092	0.726630	0.435991

8 rows × 34 columns

pd.set_option('display.max_rows', 100)
pd.set_option('display.max_columns', None)
pd.set_option('display.width', None)
pd.set_option('display.max_colwidth', None)

display(df_X.describe().T)

	count	mean	min	25%	50%	75%	max	std
date	163913	2009-07-17 14:37:46.612166400	2002-01-31 00:00:00	2005-10-31 00:00:00	2009-06-30 00:00:00	2013-03-31 00:00:00	2016-12-31 00:00:00	NaN
permno	163913.0	60452.050222	10026.0	35238.0	73139.0	84168.0	93436.0	27258.977322
re	163913.0	0.007979	-0.870345	-0.040199	0.008931	0.056648	1.597907	0.094412
rf	163913.0	0.001032	0.0	0.0	0.0002	0.0015	0.0044	0.001368
rme	163913.0	0.005875	-0.1723	-0.0183	0.0092	0.0323	0.1135	0.041751
size	163913.0	15.550336	11.501877	14.676361	15.293713	16.24026	20.388632	1.161036
value	163913.0	-0.912667	-8.756389	-1.351522	-0.850813	-0.378992	2.370495	0.782885
prof	163913.0	-1.556057	-10.213809	-2.087953	-1.34637	-0.875085	0.837982	0.965714
fscore	163913.0	4.933819	0.0	4.0	5.0	6.0	8.0	1.290275
debtiss	163913.0	0.362827	0.0	0.0	0.0	1.0	1.0	0.480817
repurch	163913.0	0.650784	0.0	0.0	1.0	1.0	1.0	0.476724
nissa	163913.0	0.701982	0.329881	0.683511	0.694598	0.702139	4.265005	0.062679
growth	163913.0	0.108029	-2.535166	0.008043	0.069293	0.156135	4.030048	0.220803
aturnover	163913.0	-0.525027	-9.784996	-0.983022	-0.351011	0.113567	2.578508	0.991602
gmargins	163913.0	0.424387	0.001052	0.247732	0.385029	0.585019	1.0	0.225407
ep	163913.0	0.040381	-3.820301	0.03121	0.049545	0.067294	0.677732	0.114934
sgrowth	163913.0	0.745931	0.098861	0.695602	0.732543	0.778532	8.217025	0.140543
lev	163913.0	0.075147	-3.810427	-0.619852	-0.011205	0.687159	4.520271	1.022683
roaa	163913.0	0.051826	-4.83761	0.018625	0.048987	0.086154	0.578345	0.082937
roea	163913.0	0.000175	-0.029224	0.000069	0.000121	0.000186	0.336472	0.00302
sp	163913.0	0.001009	0.0	0.000346	0.000632	0.00114	0.036622	0.001362
mom	163913.0	0.05646	-3.034658	-0.053369	0.069856	0.184213	2.029381	0.239901
indmom	163913.0	24.522405	1.0	14.0	24.0	35.0	49.0	12.98161
mom12	163913.0	0.100258	-3.475013	-0.049678	0.115646	0.270788	3.519333	0.318652
momrev	163913.0	0.05737	-3.055986	-0.053707	0.072849	0.191116	3.302411	0.259801
valuem	163913.0	-0.948673	-8.818536	-1.38428	-0.900369	-0.417606	2.329125	0.784227
nissm	163913.0	0.700911	0.329881	0.682923	0.694412	0.701702	2.711109	0.060812
strev	163913.0	0.014663	-0.868645	-0.035392	0.013158	0.061674	2.596567	0.095684
ivol	163913.0	0.015696	0.000463	0.009952	0.013612	0.019028	0.218682	0.008647
betaarb	163913.0	1.032455	0.24138	0.85159	1.003569	1.178665	2.350102	0.251549
indrrev	163913.0	0.006188	-0.820129	-0.033465	0.002659	0.040915	2.13488	0.07749
price	163913.0	3.664508	0.57098	3.258097	3.679082	4.06337	11.631769	0.685092
age	163913.0	5.512095	3.637586	5.003946	5.575949	6.165418	6.555357	0.72663
shvol	163913.0	1.057609	0.003904	0.748381	0.999129	1.312665	4.319359	0.435991

11.2.2.2. What are these characteristics?

• They are based on various accounting and market based information

• Each characteristic is constructed differently–we will discuss in detail a handful of them

• The construction of each signal is full of painful details and there are many details that matter

• Observation:

  • size is log market cap

  • Value is Book-to-market (Why is this called value?)

11.2.2.3. Group assets by signal

• We select our characteristic

• We now need to assign groups to each stocks. These groups will identify which portfolio each stock belongs in a particular date according to the position of the characteristic in that date

• We will do this by applying the function pd.qcut to the chosen characteristic. This will “cut” the signal distribution in the chosen number of groups.

• The important aspects is that we will applying this date by date. This make the strategy cross-sectional because you are using the distribution of the signal as given date to the grouping– Very much like curved grades by cohort

• Details

• duplicates='drop': In case there are two stocks with exactly the same signal that are exactly in the cutoff of the groups, we drop one of the observations

• labels=False: The method simply label the groups with numbers. For example if ngroups=10 then it will assign 0 to the stocks with the bottom 10% returns in a given date, 1 to stocks with returns in between 10% and 20% of the signal distribution on a given date, …, and 9 for stocks in the top 10% (signal in between 90% and 100% of the return distribution on a given date) .

X='value'
ngroups=10
df_X['X_group']=df_X.groupby(['date'])[X].transform(lambda x: pd.qcut(x, ngroups, labels=False,duplicates='drop'))
df_X[['date','permno',X,'X_group']]

	date	permno	value	X_group
0	2002-01-31	10078	-2.471709	0
1	2002-01-31	10104	-3.183480	0
2	2002-01-31	10107	-1.696643	2
3	2002-01-31	10108	-1.461118	3
4	2002-01-31	10119	-0.521094	7
...	...	...	...	...
163908	2016-12-31	93420	1.049163	9
163909	2016-12-31	93422	0.829353	9
163910	2016-12-31	93423	-2.128977	1
163911	2016-12-31	93429	-3.001095	0
163912	2016-12-31	93436	-3.328269	0

163913 rows × 4 columns

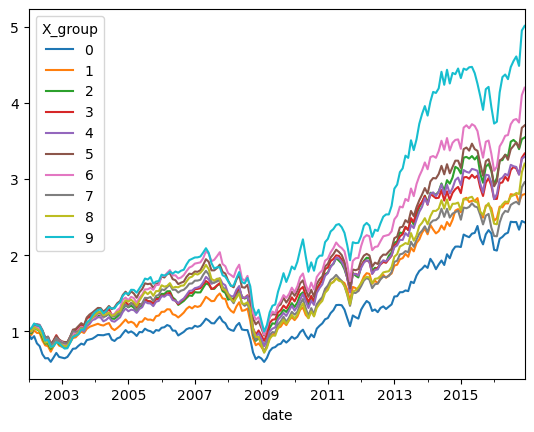
Portfolio formation tradeoffs: Diversification vs Signal Strengh

• We will start by constructing Equal weighted portfolios within each signal bucket

• Why not sort in 100 groups instead on only 10? This way your top portfolio would have much higher average characteristics

• Why no simply focus on the stock with the highest characteristic?

1. Individual stocks have \(\sigma\) = 40 − 80%, so \(\sigma/\sqrt{T}\) makes it nearly impossible to accurately measure E(R). Portfolios have lower \(\sigma\) by diversification.

2. So you have to trade-off strengh of the signal against benefits of diversification

Calculate the portfolio return

We will do market cap weights, but you could do Equal weight or even sginal weights

\[\sum_i^I w_{it} r_{it}\]

Where the weights must add up to 1.

Before forming portfolios we will use the risk-free rate so we form fully invested portfolios. So the ouput will be returns and not excess returns

Equal weighted returns

ret_byX_ew =df_X.groupby(['date','X_group']).re.mean()
ret_byX_ew=ret_byX_ew.unstack(level=-1)
(ret_byX_ew+1).cumprod().plot()

<Axes: xlabel='date'>

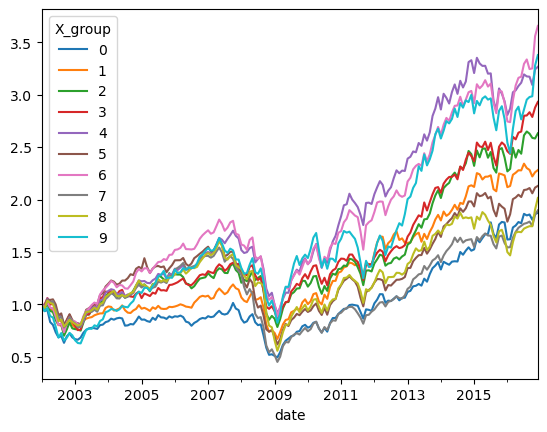
Market cap weighted returns

print(df_X['size']) 
print(df_X.size)

0         17.748484
1         18.481351
2         19.789216
3         15.902263
4         14.275648
            ...    
163908    14.337515
163909    15.256946
163910    15.502888
163911    15.504722
163912    17.262975
Name: size, Length: 163913, dtype: float64

df_X['me_l1']=np.exp(df_X['size'])
ret_byX_vw =df_X.groupby(['date','X_group']).apply(lambda x:(x.re*x.me_l1).sum()/x.me_l1.sum())
ret_byX_vw=ret_byX_vw.unstack(level=-1)
(ret_byX_vw+1).cumprod().plot()

C:\Users\alan.moreira\AppData\Local\Temp\ipykernel_24324\2208835029.py:2: DeprecationWarning: DataFrameGroupBy.apply operated on the grouping columns. This behavior is deprecated, and in a future version of pandas the grouping columns will be excluded from the operation. Either pass `include_groups=False` to exclude the groupings or explicitly select the grouping columns after groupby to silence this warning.
  ret_byX_vw =df_X.groupby(['date','X_group']).apply(lambda x:(x.re*x.me_l1).sum()/x.me_l1.sum())

<Axes: xlabel='date'>

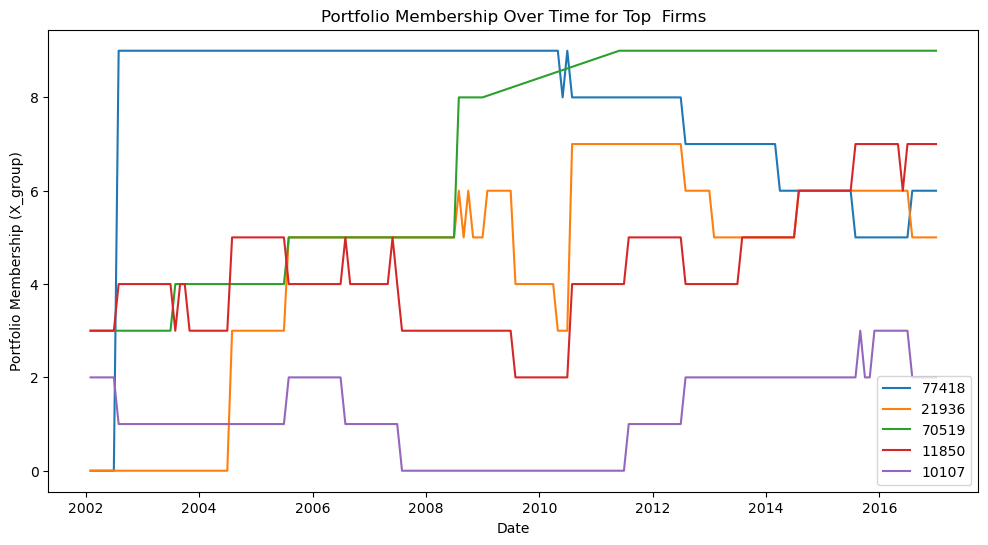
If we focus on a particular stock, we can see how it’s portfolio membership changed over time.

You can check you that some characteristics are fairly persistent and change only slowly over time

While others, like momentum change very frequently.

_temp=df_X.sort_values(by=['date','size'])
top=_temp[_temp.date=='2002-01-31'].tail(5).permno.tolist()
top

[77418, 21936, 70519, 11850, 10107]

plt.figure(figsize=(12,6))
for firm in top:
    data = df_X[df_X.permno==firm][['date','X_group']]
    plt.plot(data['date'], data['X_group'], label=str(firm))
plt.xlabel('Date')
plt.ylabel('Portfolio Membership (X_group)')
plt.title('Portfolio Membership Over Time for Top  Firms')
plt.legend()
plt.show()

Things to try

• Play with different number of groups, how the spread in X across portfolios change? How the volatility of the individual portfolios change?

• Look at different characteristics. Which ones create higher spread in average returns

• Construct the long-short portfolio that goes long the high portfolio and short the low portfolio. What are the properties of this portfolio?

• Which ones have alpha relative to the market in the sample? What do their betas look like

• When they perform poorly?

• How correlated are the returns of the long-shorts of different characteristics?

---

📝 Key Takeaways

• Stacked data frames are the backbone when working with thousands of stocks and multiple characteristics.

• Lagged market-cap weights should be the default: they minimize turnover, reflect realistic trading capacity, and eliminate look-ahead bias.

• Characteristic-sorted portfolios isolate cross-sectional spreads in the signal; the long-short “top minus bottom” position delivers a clean test of the signal’s pricing power.

• Portfolio design choices matter: more groups widen the average-return spread but shrink the number of stocks per bucket; equal-weighting boosts the influence of small caps, while value-weighting is closer to how real money is run.

• A single, well-structured function automates experimentation across different signals, making it easy to investigate which characteristics generate higher alpha, when they underperform, and how their long-short returns co-move.

• The core tension is signal strength versus diversification: stronger signals often come with higher concentration and trading costs, so practical implementation always balances these forces.

---