Show code cell content

Hide code cell content

import numpy as np
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
import statsmodels.api as sm
!pip install wrds
import wrds
import pandas_datareader.data as web

def get_factors(factors='CAPM',freq='daily'):   
    
    if freq=='monthly':
        freq_label=''
    else:
        freq_label='_'+freq


    if factors=='CAPM':
        fama_french = web.DataReader("F-F_Research_Data_Factors"+freq_label, "famafrench",start="1921-01-01")
        daily_data = fama_french[0]
    
     
        df_factor = daily_data[['RF','Mkt-RF']] 
    elif factors=='FF3':
        fama_french = web.DataReader("F-F_Research_Data_Factors"+freq_label, "famafrench",start="1921-01-01")
        daily_data = fama_french[0]

        df_factor = daily_data[['RF','Mkt-RF','SMB','HML']]
    elif factors=='FF5':

        fama_french = web.DataReader("F-F_Research_Data_Factors"+freq_label, "famafrench",start="1921-01-01")
        daily_data = fama_french[0]

        df_factor = daily_data[['RF','Mkt-RF','SMB','HML']]
        fama_french2 = web.DataReader("F-F_Research_Data_5_Factors_2x3"+freq_label, "famafrench",start="1921-01-01")
        daily_data2 = fama_french2[0]

        df_factor2 = daily_data2[['RMW','CMA']]
        df_factor=df_factor.merge(df_factor2,on='Date',how='outer')    
        
    else:
        fama_french = web.DataReader("F-F_Research_Data_Factors"+freq_label, "famafrench",start="1921-01-01")
        daily_data = fama_french[0]

        df_factor = daily_data[['RF','Mkt-RF','SMB','HML']]
        fama_french2 = web.DataReader("F-F_Research_Data_5_Factors_2x3"+freq_label, "famafrench",start="1921-01-01")
        daily_data2 = fama_french2[0]

        df_factor2 = daily_data2[['RMW','CMA']]
        df_factor=df_factor.merge(df_factor2,on='Date',how='outer')   
        fama_french = web.DataReader("F-F_Momentum_Factor"+freq_label, "famafrench",start="1921-01-01")
        df_factor=df_factor.merge(fama_french[0],on='Date')
        df_factor.columns=['RF','Mkt-RF','SMB','HML','RMW','CMA','MOM']    
    if freq=='monthly':
        df_factor.index = pd.to_datetime(df_factor.index.to_timestamp())
    else:
        df_factor.index = pd.to_datetime(df_factor.index)
        


    return df_factor/100

def get_daily_wrds_multiple_ticker(tickers,conn):
  
    # Retrieve PERMNOs for the specified tickers
    permnos = conn.get_table(library='crsp', table='stocknames', columns=['permno', 'ticker', 'namedt', 'nameenddt'])
    permnos['nameenddt']=pd.to_datetime(permnos['nameenddt'])
    permnos = permnos[(permnos['ticker'].isin(tickers)) & (permnos['nameenddt']==permnos['nameenddt'].max())]
    # Extract unique PERMNOs
    permno_list = permnos['permno'].unique().tolist()
    print(permno_list)

    # Query daily stock file for the specified PERMNOs
    query = f"""
        SELECT permno, date, ret, retx, prc       
        FROM crsp.dsf
        WHERE permno IN ({','.join(map(str, permno_list))})
        ORDER BY date
    """
    daily_returns = conn.raw_sql(query, date_cols=['date'])
    daily_returns = daily_returns.merge(permnos[['permno', 'ticker']], on='permno', how='left')
    # Pivot data to have dates as index and tickers as columns
    daily_returns = daily_returns.pivot(index='date', columns='ticker', values='ret')    
    daily_returns=daily_returns[tickers]



    return daily_returns


    
def get_permnos(tickers,conn):
  
    # Retrieve PERMNOs for the specified tickers
    permnos = conn.get_table(library='crsp', table='stocknames', columns=['permno', 'ticker', 'namedt', 'nameenddt'])
    permnos['nameenddt']=pd.to_datetime(permnos['nameenddt'])
    permnos = permnos[(permnos['ticker'].isin(tickers)) ]
    



    return permnos

13. Multi-factor models

---

🎯 Learning Objectives

By the end of this chapter, you should be able to:

1. Understand why investors move beyond CAPM.
   Explain how adding multiple systematic factors (size, value, profitability, investment, momentum, etc.) sharpens alpha measurement, improves risk control, and better reflects real‐world return drivers.

2. Estimate factor betas with a time-series regression.
   Learn to regress an asset’s excess returns on a panel of factor returns, interpret coefficients as exposures, and judge statistical reliability.

3. Translate betas into economic insight through variance decomposition.
   Decompose each asset’s total variance into contributions from individual factors and idiosyncratic noise, revealing which risks truly matter.

4. Build cleaner covariance matrices using a factor structure.
   Combine factor loadings with the factor covariance matrix and asset-specific variances to obtain a stable, low-dimensional estimate suitable for portfolio optimization.

5. Apply multi-factor analysis to real portfolios and ETFs.
   Perform step-by-step alpha/beta evaluation of momentum ETFs, ranking funds on both skill (alpha) and risk profile.

6. Attribute portfolio risk when holdings change.
   Project how reallocating capital between strategies alters overall volatility, using factor exposures rather than naïve variance estimates.

7. Contrast top-down versus bottom-up factor measurement.
   Weigh the pros and cons of estimating betas from portfolio returns versus aggregating betas of individual holdings.

8. Explore the characteristic-based (cross-sectional) alternative.
   See how pricing firm-level attributes with cross-sectional regressions yields “characteristic-implied” returns and characteristic-adjusted performance.

---

So far we have focused on the market as our single factor.

In practice it is standard to use factor models with many factors

Additional factors

• soak up risk making measure of alpha easier

• Difference out other sources of expected excess returns that are easy to get access to

• Allows for better risk management

We deal with this, by simply adding more factors to our model. Say we now have \(m\) different factors

\[r_t^i=b_{i,1}f_t^1+b_{i,2}f_t^2+b_{i,3}f_t^3+...+b_{i,m}f_t^m+\epsilon_{i,t}\]

Where \(b_{i,j}\) measures the exposure of asset \(i\) to factor \(j\)

IF we stack these exposures in a m by 1 vector \(B_i=[b_{i,1},b_{i,2},...b_{i,M}]\) and the factors in a m by 1 vector \(F_t=[f^1_t,f^2_t,...,f^m_t]\) we can write this in matrix notation

\[r_t^i=B_i@F_t+u_{i,t}\]

As before we can also stack the individual returns :

\[R_t=B@F_t+U_t\]

where

• \(R_t\) is a n by 1 vector with the excess returns of the n assets

• \(B\) is n by m matrix where each row has the exposure of an asset with respect to each M factor and each column has the exposures of the different assets with respect to a particular factor

• \(U_t\) as before is a n by 1 vector with the residual risk of each asset

“Endogenous” Benchmarking

• it is common for large portfolio allocators to set benchmarks for the managers that they allocate to

• The most common benchmark is simply returns of the S&P500 which is almost the same thing as the returns of the market portfolio ( large caps dominate the returns of any market-cap portfolio)

• You might also have endogenous benchmarks

• Use a set of Factors F and estimate \(r^b_t=\sum \beta_j F_{j,t}\)

• I.e use as a bechmark the multifactor combination that best replicates the portfolio.

• typically this is not done contractually but implicitly: You will allocate to the different funds based on their alpha

• Captures the idea that one should pay different prices for alpha (very hard to get) and beta( easier, the gains are in implementation)

13.1. Estimating a multi-factor model: The Time-series approach

We start with the factors and estimate the betas using time-series data

This works particularly well when the factors are excess returns themselves

For each asset We run a tim-series regression with the excess returns of the asset as the the dependent variable and the excess returns on the factors as the independent variables

13.2. Application

What do you get when you invest in a Momentum ETF?

1. Get daily return data on the larger ETFs claiming to implement the momentum factor

2. Get factors excess returns: Market, Size (SMB), Value (HML), Profitability (RMW), Investment (CMA) , and Momentum (MOM)

3. Run a time series regression for each ETF on the factors

4. Look at alphas and betas

tickers = ["MTUM", "SPMO", "XMMO", "IMTM", "XSMO", "PDP", "JMOM", "DWAS", "VFMO", "XSVM", "QMOM"]
conn=wrds.Connection()
# Get daily returns for the specified tickers
df_ETF=get_daily_wrds_multiple_ticker(tickers,conn)
# Get daily factors
df_factor=get_factors('FF6','daily')
# Align the dataframes
df_ETF, df_factor = df_ETF.align(df_factor, join='inner', axis=0)
# Subtract risk-free rate from ETF returns
df_ETF=df_ETF.subtract(df_factor['RF'],axis=0)

WRDS recommends setting up a .pgpass file.
Created .pgpass file successfully.
You can create this file yourself at any time with the create_pgpass_file() function.
Loading library list...
Done
[13512, 13851, 15161, 15725, 17085, 17392, 17622, 90621, 90622, 90623, 91876]

import statsmodels.api as sm

X = df_factor.drop(columns=['RF'])
X = sm.add_constant(X)  # Adds a constant term to the predictor
y = df_ETF[tickers[1]]
X=X[y.isna()==False]
y=y[y.isna()==False]
model = sm.OLS(y, X).fit(dropna=True)
print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   SPMO   R-squared:                       0.867
Model:                            OLS   Adj. R-squared:                  0.867
Method:                 Least Squares   F-statistic:                     2242.
Date:                Tue, 21 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:34:16   Log-Likelihood:                 8217.0
No. Observations:                2069   AIC:                        -1.642e+04
Df Residuals:                    2062   BIC:                        -1.638e+04
Df Model:                           6                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const       4.572e-05      0.000      0.454      0.650      -0.000       0.000
Mkt-RF         0.9997      0.009    109.378      0.000       0.982       1.018
SMB           -0.1673      0.017     -9.581      0.000      -0.202      -0.133
HML           -0.0388      0.016     -2.477      0.013      -0.070      -0.008
RMW           -0.0243      0.022     -1.110      0.267      -0.067       0.019
CMA            0.0761      0.030      2.560      0.011       0.018       0.134
MOM            0.2453      0.010     24.599      0.000       0.226       0.265
==============================================================================
Omnibus:                      317.585   Durbin-Watson:                   2.150
Prob(Omnibus):                  0.000   Jarque-Bera (JB):             3941.046
Skew:                           0.282   Prob(JB):                         0.00
Kurtosis:                       9.738   Cond. No.                         318.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Results=pd.DataFrame([],index=tickers,columns=X.columns)
for ticker in tickers:
    y = df_ETF[ticker]
    X = df_factor.drop(columns=['RF'])
    X = sm.add_constant(X) 
    X=X[y.isna()==False]
    y=y[y.isna()==False]
    model = sm.OLS(y, X).fit(dropna=True)
    Results.loc[ticker,:]=model.params
    Results.at[ticker,'t_alpha']=model.tvalues['const']
    Results.at[ticker,'ivol']=model.resid.std()*252**0.5
    #Results.at[ticker,X.columns[1:]]=model.params[X.columns[1:]]

Results.loc[:,'const']=Results.loc[:,'const']*252
Results.rename(columns={'const':'alpha'},inplace=True)
Results=Results[['alpha','t_alpha','Mkt-RF','SMB','HML','RMW','CMA','MOM','ivol']]
Results

	alpha	t_alpha	Mkt-RF	SMB	HML	RMW	CMA	MOM	ivol
MTUM	-0.005012	-0.300789	1.01803	-0.107	-0.062138	-0.117292	-0.011854	0.316422	0.054317
SPMO	0.011521	0.454353	0.999749	-0.167316	-0.038834	-0.024316	0.076116	0.245338	0.072404
XMMO	0.006211	0.322732	1.043315	0.320758	0.020201	0.030898	-0.090631	0.193039	0.083264
IMTM	-0.028412	-0.849759	0.798808	-0.019567	0.075919	-0.126253	0.078522	0.127906	0.099686
XSMO	-0.011826	-0.570276	0.987091	0.846153	0.173362	0.084136	-0.077522	0.161215	0.089721
PDP	-0.012504	-0.811631	1.054572	0.138325	-0.006651	-0.079877	-0.205302	0.252667	0.063018
JMOM	0.006281	0.276272	0.963352	0.007072	-0.07626	-0.07507	-0.052893	0.099189	0.056012
DWAS	-0.001649	-0.076007	1.093378	1.079318	0.233582	-0.230806	-0.087208	0.408747	0.073130
VFMO	0.018697	0.859105	1.030837	0.446082	0.183954	-0.222156	-0.053664	0.396948	0.052463
XSVM	-0.002226	-0.115417	0.935784	0.977751	0.502337	0.319454	0.254056	-0.064561	0.083454
QMOM	0.010592	0.229192	1.080628	0.497064	0.131608	-0.380951	-0.116392	0.577498	0.130752

How should we evaluate these funds?

Which fund is “better”? Is it all about alpha in this case?

What are other things that we should be looking at?

Is this table providing a fair comparison across funds?

13.3. Variance decomposition

The betas measure the exposure of the asset return to the factor, but it does not give an accurate way of thinking which factor drives the most of the variation in the asset as factors can have very different variances

\[1=\frac{Cov(r^i_t,r^i_t)}{Var(r^i_t)}=\frac{Cov(r^i_t,\sum_j^m \beta_{i,j}f^j_t+\epsilon^i_t)}{Var(r^i_t)}\]

\[1=\frac{\sum_j^m \beta_{i,j}Cov(r^i_t,f^j_t)+\sigma^2_{\epsilon}}{Var(r^i_t)}\]

The the variance share of factor j is \(\frac{\beta_{i,j}Cov(r^i_t,f^j_t)}{Var(r^i_t)}\) and the share of non-factor variance is \(\frac{\sigma^2_{\epsilon}}{Var(r^i_t)}\)

VarianceDecomposition=pd.DataFrame([],index=tickers,columns=X.columns[1:])
FactorLoadings=pd.DataFrame([],index=tickers,columns=X.columns[1:])
VarianceIdiosyncratic=pd.DataFrame([],index=tickers,columns=['epsilon'])
for ticker in tickers:
    y = df_ETF[ticker]
    Factors = df_factor.drop(columns=['RF'])
    X = sm.add_constant(Factors) 
    X=X[y.isna()==False]
    y=y[y.isna()==False]
    model = sm.OLS(y, X).fit(dropna=True)
    # get the covariance matrix of the factors and the dependent variable
    CovMatrix=pd.concat([y,X.iloc[:,1:]],axis=1).cov()
    # get the column of the covariance matrix corresponding to the dependent variable and exclude itself to get the covariance of 
    # the dependent variable with each factor
    FactorLoadings.loc[ticker,:]=model.params[1:]
    VarianceIdiosyncratic.loc[ticker,'epsilon']=model.resid.var()
    VarianceDecomposition.loc[ticker,:]=model.params[1:]*CovMatrix.iloc[1:,0]/y.var()*100
    # Get the residual variance
    VarianceDecomposition.at[ticker,'epsilon']=model.resid.var()/y.var()*100



np.floor(VarianceDecomposition)

	Mkt-RF	SMB	HML	RMW	CMA	MOM	epsilon
MTUM	85	-1	0	1	0	4	8.0
SPMO	85	-1	0	0	-1	2	13.0
XMMO	83	4	0	-1	0	-2	13.0
IMTM	68	-1	-1	1	-1	-1	31.0
XSMO	70	16	1	-1	0	-3	14.0
PDP	90	1	-1	0	1	-2	7.0
JMOM	90	0	1	0	0	-1	6.0
DWAS	64	23	-1	2	0	1	8.0
VFMO	82	7	-2	2	0	2	4.0
XSVM	60	18	10	-2	0	1	10.0
QMOM	58	6	-2	3	0	7	23.0

What do we learn?

Decompositions like that extensively in the money management industry

• Used to classify managers in terms of styles–often called style analysis

• Used to control own portfolio factor risk to satisfy investment mandates

When looking at a portfolio/fund you have two approaches to measure it’s factor exposures

• Top down: what we did so far. run a time-series regression of the portfolio returns on the factor return

• Bottom up: from the asset factor exposures build the portfolio factor exposure

What are the benefits and drawbacks of each?

13.4. Application: A better behaved co-variance matrix

We have

\[R_t=B@F_t+u_t\]

Then

\[Var(R_t)=B@Var(F_t)@B.T+Var(U_t)\]

The big difference is that now \(F\) is a vector of factors

so \(Var(F_t)\) is a M by M variance covariance matrix, where M is the number of factors

Var_F=Factors.cov()
Cov=FactorLoadings @ Var_F @ FactorLoadings.T + np.diag(VarianceIdiosyncratic.values.reshape(-1))
Cov

	MTUM	SPMO	XMMO	IMTM	XSMO	PDP	JMOM	DWAS	VFMO	XSVM	QMOM
MTUM	0.00016	0.000143	0.000155	0.000117	0.000152	0.000158	0.000141	0.000175	0.000159	0.000139	0.000169
SPMO	0.000143	0.000159	0.00015	0.000114	0.000146	0.000152	0.000137	0.000166	0.000152	0.000138	0.00016
XMMO	0.000155	0.00015	0.0002	0.000127	0.000178	0.000171	0.000153	0.000203	0.000175	0.000173	0.000184
IMTM	0.000117	0.000114	0.000127	0.000136	0.000128	0.000127	0.000115	0.000144	0.000129	0.000127	0.000133
XSMO	0.000152	0.000146	0.000178	0.000128	0.000227	0.000173	0.000154	0.000223	0.000184	0.000198	0.000192
PDP	0.000158	0.000152	0.000171	0.000127	0.000173	0.000187	0.000154	0.000198	0.000174	0.000163	0.000184
JMOM	0.000141	0.000137	0.000153	0.000115	0.000154	0.000154	0.000152	0.000173	0.000154	0.000148	0.00016
DWAS	0.000175	0.000166	0.000203	0.000144	0.000223	0.000198	0.000173	0.000284	0.000215	0.000218	0.000229
VFMO	0.000159	0.000152	0.000175	0.000129	0.000184	0.000174	0.000154	0.000215	0.000195	0.000177	0.000196
XSVM	0.000139	0.000138	0.000173	0.000127	0.000198	0.000163	0.000148	0.000218	0.000177	0.000252	0.000175
QMOM	0.000169	0.00016	0.000184	0.000133	0.000192	0.000184	0.00016	0.000229	0.000196	0.000175	0.000281

Suppose you are trying to construct the minimum variance portfolio–say you think expected returns are undistinguishable across the funds, so you simply want to minimize variance

your optimal weight, if you knew the covariance matrix is

\[E[R^e]Var(R^e)^{-1}\]

• If we compare the in-sample Variance of our minimum variance portfolios for

  • The unrestricted case

  • The single-factor covariance

  • The multi-factor covariance

• which one will have lowest variance? What will have the highest?

• Now split the sample in two. Repeat the covariance estimation procedure for each of these approaches for the first half of the sample

• Now use the weights to compute the variance of each of the portfolios in the second half

• Is the order likely to change? Why? Why not?

13.5. Application: How will your portfolio risk change as you add positions

You have portfolio \(X_0\) and you want to sell w of your positions to invest in a fund with portfolio \(X_1\). How your portfolio variance will change as a function of you reallocation?

• The answer is simple

\[Var(wX_1R_t+(1-w)X_0R_t)-Var(X_0R_t)\]

• But also kind of misleading since you might not have good data to estimate the variance of the new portfolio

• Now if you know each portfolio factor betas,\(\beta_0=X_0@B\) and \(\beta_1=X_1@B\) , and at least one of this portfolio is large and well diversified, then for small tilts, i.e. \(w\) small, we have

\[\frac{Var(wX_1R_t+(1-w)X_0R_t)-Var(X_0R_t)}{\Delta w}|_{w\approx 0} =\beta_1Var(F)\beta_0'\]

• The fact that one is well diversified just means that you can ignore the covariance-terms of the portfolios asset specific risks

• So you see above why a large pool of money when allocating money to an active manager will want to regulate their factor exposure

• funds with similar volatilities will be perceived as very different risks depending on how the exposure of portfolio relates to the exposure of the fund

For example, look at how your portfolio risk change if you go from an equal weighted portfolio of these ETFS to just investing in one of them, say MTUM

13.6. Performance Attribution

• We can use factor models to decompose a manager strategy

• What explains their returns?

• What tilts they have? What kind of stocks they like?

13.6.1. Application: What does Cathie Wood Likes ?

Cathie Wood is a renowned stock-picker and the founder of ARK Invest, which manages around 60 billion in assets and invests in innovative technologies such as self-driving cars and genomics. She gained fame for her success in the male-dominated world of investing, her persuasive investment arguments, and her proven track record in the stock market. Prior to founding ARK Invest, she gained experience at The Capital Group, Jennison Associates, and AllianceBernstein, and co-founded Tupelo Capital Management, a hedge fund. Wood is known for her unconventional investment strategies and her advocacy for investing in disruptive technologies, which has garnered her a large following in the investing world. Her estimated net worth is around $250 million.

Citations: https://www.nytimes.com/2021/08/22/business/cathie-wood-ark-stocks.html

df=pd.read_pickle('https://raw.githubusercontent.com/amoreira2/Fin418/main/assets/data/df_WarrenBAndCathieW.pkl')
_temp=df.dropna()
# select the columns to use as factors
Factors=_temp.drop(['BRK','RF','ARKK'],axis=1)
ArK=_temp.ARKK-_temp.RF

What are these factors?

• HML is the value strategy that buys high book to market firms and sell low book to market firms

• SMB is a size strategy that buys firms with low market capitalization and sell firms with high market capitalizations

• RmW is the strategy that buys firms with high gross profitability and sell firms with low gross profitability

• CmA is the strategy that buys firms that are investing little (low CAPEX) and sell firms that are investing a lot (high CAPEX)

• MOM is the momentum strategy that buy stocks that did well in the last 12 months and short the ones that did poorly

We will discuss more later

for now just think of them as important trading strategies that practicioners know

x= sm.add_constant(Factors)
y= ArK
results= sm.OLS(y,x).fit()
results.summary()

OLS Regression Results

Dep. Variable:	y	R-squared:	0.781
Model:	OLS	Adj. R-squared:	0.780
Method:	Least Squares	F-statistic:	1069.
Date:	Thu, 28 Mar 2024	Prob (F-statistic):	0.00
Time:	16:24:08	Log-Likelihood:	5908.9
No. Observations:	1804	AIC:	-1.180e+04
Df Residuals:	1797	BIC:	-1.177e+04
Df Model:	6
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
const	0.0004	0.000	1.821	0.069	-3.03e-05	0.001
Mkt-RF	1.1736	0.020	58.714	0.000	1.134	1.213
SMB	0.6944	0.037	18.984	0.000	0.623	0.766
HML	-0.6521	0.038	-16.938	0.000	-0.728	-0.577
RMW	-0.9037	0.054	-16.883	0.000	-1.009	-0.799
CMA	-0.5034	0.071	-7.129	0.000	-0.642	-0.365
Mom	-0.0397	0.025	-1.559	0.119	-0.090	0.010

Omnibus:	55.310	Durbin-Watson:	2.135
Prob(Omnibus):	0.000	Jarque-Bera (JB):	128.873
Skew:	0.116	Prob(JB):	1.04e-28
Kurtosis:	4.289	Cond. No.	345.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

• How much can we explain of ARKK return behavior?

• What kind of stocks CW likes?

• How much of her portfolio variance comes from market exposure alone?

• If you were to construct a replicating portfolio of her fund

• What would be the volatility of your residual risk?

13.7. Bottom up: from assets factor risk to portfolio factor risk

Above we estimated fund factor exposures by looking at how the fund co-move with the different factors

An alternative is to look through the fund and compute asset factor loadings and from them compute the fund factor loadings

Consider portfolio with weights \(X\) that earns excess returns \(r=X@R\) where R is the vector of asset excess returns.

Asset’s excess returns satisfy a factor model

\[R=A+B@F+U\]

then the portfolio satisfies

\[r=X@R=X@(A+B@F+U)=X@A+X@B@F+X@U\]

In scalar notation this is simply

\[r=\sum_i x_i r_i=\sum_i x_i\alpha_i+ \sum_j \sum_i x_i \beta_{i,j}f_j+\sum_i x_i\epsilon_i\]

So the portfolio exposure to factor j is simply the dollar-weighted average of the asset betas

\[\beta_{p,j}=\sum_i x_i \beta_{i,j}\]

• For portfolios with high turnover, this approach will lead to better measurement of factor risk

• For portfolios that do not trade, then measuring individual asset betas might introduce unnecessary noise and extra work

import pandas as pd

date1='2014-12-31'
date2='2015-12-31'
date3='2016-12-31'
# Define the portfolio data
portfolio_data1 = {
    'date': [date1,date1,date1,date1,date1],
    'ticker': ['AAPL', 'GOOGL', 'MSFT','NVDA','AMZN'],
    'weight': [0.2,0.2, 0.2,0.2,0.2]
}

portfolio_data2 = {
    'date': [date2,date2,date2,date2],
    'ticker': ['COST', 'WMT', 'TGT','KR'],
    'weight': [0.25,0.25, 0.25,0.25]
}
# Concatenate the two dataframes
portfolio_df1 = pd.DataFrame(portfolio_data1)
portfolio_df2 = pd.DataFrame(portfolio_data2)

# Generate monthly dates from date1 to date2 and from date2 to now
date_range1 = pd.date_range(start=date1, end=date2, freq='B')
date_range2 = pd.date_range(start=date2, end=date3, freq='B')

# Create monthly dataframes for each portfolio
monthly_portfolio1 = pd.DataFrame(
    [(date, ticker, weight) for date in date_range1 for ticker, weight in zip(portfolio_df1['ticker'], portfolio_df1['weight'])],
    columns=['date', 'ticker', 'weight']
)
monthly_portfolio2 = pd.DataFrame(
    [(date, ticker, weight) for date in date_range2 for ticker, weight in zip(portfolio_df2['ticker'], portfolio_df2['weight'])],
    columns=['date', 'ticker', 'weight']
)

# Combine the monthly dataframes
final_portfolio_df = pd.concat([monthly_portfolio1, monthly_portfolio2], ignore_index=True)

# import ace_tools as tools
# tools.display_dataframe_to_user(name="Portfolio Monthly Weights", dataframe=final_portfolio_df)

final_portfolio_df 

	date	ticker	weight
0	2014-12-31	AAPL	0.20
1	2014-12-31	GOOGL	0.20
2	2014-12-31	MSFT	0.20
3	2014-12-31	NVDA	0.20
4	2014-12-31	AMZN	0.20
...	...	...	...
2353	2016-12-29	KR	0.25
2354	2016-12-30	COST	0.25
2355	2016-12-30	WMT	0.25
2356	2016-12-30	TGT	0.25
2357	2016-12-30	KR	0.25

2358 rows × 3 columns

tickers = final_portfolio_df.ticker.unique().tolist()    
#conn=wrds.Connection()
# Get daily returns for the specified tickers
df_stocks=get_daily_wrds_multiple_ticker(tickers,conn)
# Get daily factors
df_factor=get_factors('FF6','daily')
df_factor=df_factor.dropna()
# Align the dataframes

# Subtract risk-free rate from ETF returns
df_stocks=df_stocks.subtract(df_factor['RF'],axis=0)
df_stocks

[10107, 14593, 16678, 49154, 55976, 84788, 86580, 87055, 90319]

ticker	AAPL	GOOGL	MSFT	NVDA	AMZN	COST	WMT	TGT	KR
1928-01-26	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1928-01-27	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1928-01-28	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1928-01-30	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1928-01-31	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
...	...	...	...	...	...	...	...	...	...
2024-11-22	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2024-11-25	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2024-11-26	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2024-11-27	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2024-11-29	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

25409 rows × 9 columns

df=df_stocks.stack()
df.name='eret'
df=final_portfolio_df.merge(df,left_on=['date','ticker'],right_index=True,how='left')
df

	date	ticker	weight	eret
0	2014-12-31	AAPL	0.20	-0.019019
1	2014-12-31	GOOGL	0.20	-0.008631
2	2014-12-31	MSFT	0.20	-0.012123
3	2014-12-31	NVDA	0.20	-0.015710
4	2014-12-31	AMZN	0.20	0.000161
...	...	...	...	...
2353	2016-12-29	KR	0.25	-0.002605
2354	2016-12-30	COST	0.25	-0.006340
2355	2016-12-30	WMT	0.25	-0.002031
2356	2016-12-30	TGT	0.25	-0.005380
2357	2016-12-30	KR	0.25	-0.002323

2358 rows × 4 columns

TOP DOWN

For comparison lets estimate this fund factor exposure using the top down approach

Lets construct the portfolio return and then run the multi-factor regression

fund_return=df.groupby('date').apply(lambda x: (x['eret']*x['weight']).sum() )
df_factor, fund_return = df_factor.align(fund_return, join='inner', axis=0)

y=fund_return.copy()
X = df_factor.drop(columns=['RF'])
X = sm.add_constant(X) 
X=X[y.isna()==False]
y=y[y.isna()==False]
model = sm.OLS(y, X).fit(dropna=True)
model.summary()

OLS Regression Results

Dep. Variable:	y	R-squared:	0.533
Model:	OLS	Adj. R-squared:	0.527
Method:	Least Squares	F-statistic:	94.64
Date:	Thu, 16 Jan 2025	Prob (F-statistic):	4.66e-79
Time:	17:16:05	Log-Likelihood:	1711.9
No. Observations:	505	AIC:	-3410.
Df Residuals:	498	BIC:	-3380.
Df Model:	6
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
const	0.0005	0.000	1.490	0.137	-0.000	0.001
Mkt-RF	0.9562	0.044	21.531	0.000	0.869	1.043
SMB	-0.1387	0.080	-1.732	0.084	-0.296	0.019
HML	-0.0802	0.097	-0.830	0.407	-0.270	0.109
RMW	0.6811	0.116	5.847	0.000	0.452	0.910
CMA	-0.4294	0.150	-2.855	0.004	-0.725	-0.134
MOM	0.1413	0.050	2.836	0.005	0.043	0.239

Omnibus:	99.867	Durbin-Watson:	1.935
Prob(Omnibus):	0.000	Jarque-Bera (JB):	369.570
Skew:	0.859	Prob(JB):	5.61e-81
Kurtosis:	6.822	Cond. No.	455.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Now suppose you know the time of the portfolio change

I can break the regression, but what do I loose?

    y=fund_return.copy()
    X = df_factor.drop(columns=['RF'])
    y=y[:'2015-12-31']
    X=X[:'2015-12-31']
    
    X = sm.add_constant(X) 
    X=X[y.isna()==False]
    y=y[y.isna()==False]
    model = sm.OLS(y, X).fit(dropna=True)
    display(model.summary())

    
    y=fund_return.copy()
    X = df_factor.drop(columns=['RF'])
    y=y['2015-12-31':]
    X=X['2015-12-31':]
    
    X = sm.add_constant(X) 
    X=X[y.isna()==False]
    y=y[y.isna()==False]
    model = sm.OLS(y, X).fit(dropna=True)
    model.summary()

OLS Regression Results

Dep. Variable:	y	R-squared:	0.766
Model:	OLS	Adj. R-squared:	0.760
Method:	Least Squares	F-statistic:	134.0
Date:	Thu, 16 Jan 2025	Prob (F-statistic):	1.33e-74
Time:	17:16:07	Log-Likelihood:	905.06
No. Observations:	253	AIC:	-1796.
Df Residuals:	246	BIC:	-1771.
Df Model:	6
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
const	0.0009	0.000	2.041	0.042	3.1e-05	0.002
Mkt-RF	1.0240	0.048	21.290	0.000	0.929	1.119
SMB	-0.2619	0.102	-2.579	0.011	-0.462	-0.062
HML	0.1045	0.129	0.812	0.418	-0.149	0.358
RMW	0.6329	0.168	3.758	0.000	0.301	0.965
CMA	-2.0804	0.229	-9.083	0.000	-2.532	-1.629
MOM	-0.0701	0.063	-1.106	0.270	-0.195	0.055

Omnibus:	88.712	Durbin-Watson:	1.815
Prob(Omnibus):	0.000	Jarque-Bera (JB):	385.398
Skew:	1.374	Prob(JB):	2.05e-84
Kurtosis:	8.386	Cond. No.	576.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

OLS Regression Results

Dep. Variable:	y	R-squared:	0.334
Model:	OLS	Adj. R-squared:	0.318
Method:	Least Squares	F-statistic:	20.60
Date:	Thu, 16 Jan 2025	Prob (F-statistic):	1.61e-19
Time:	17:16:07	Log-Likelihood:	870.18
No. Observations:	253	AIC:	-1726.
Df Residuals:	246	BIC:	-1702.
Df Model:	6
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
const	-0.0004	0.001	-0.711	0.478	-0.001	0.001
Mkt-RF	0.7255	0.071	10.272	0.000	0.586	0.865
SMB	0.1198	0.108	1.105	0.270	-0.094	0.333
HML	-0.0642	0.120	-0.536	0.592	-0.300	0.172
RMW	0.7451	0.142	5.230	0.000	0.465	1.026
CMA	0.1497	0.177	0.847	0.398	-0.198	0.498
MOM	0.1587	0.069	2.313	0.022	0.024	0.294

Omnibus:	7.465	Durbin-Watson:	2.104
Prob(Omnibus):	0.024	Jarque-Bera (JB):	12.149
Skew:	-0.092	Prob(JB):	0.00230
Kurtosis:	4.058	Cond. No.	403.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Strategy Abnormal returns

Armed with betas we can construct the fund abnormal returns by simply taking out the part of the performance that is due to factor exposures

\[R_t-\sum_i\beta_i f^i_t\]

abnormal_return=fund_return-df_factor.drop(columns=['RF'])@model.params[1:]

fund_return.plot()
abnormal_return.plot()

<AxesSubplot:>

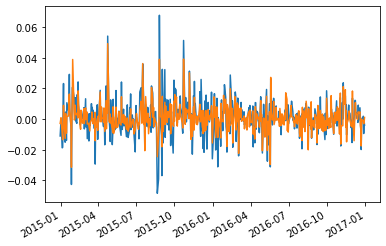
• How can you produce the abnormal returns more easily simply using outputs from the regression you just run?

• Tip: what regression statistic is equal to the average of the abormal return

Bottom UP

• Now we estimate the factor loadings for each stock

• use our beautiful linear algebra to compute fund exposures

# estimating Factor Betas
df_factor, df_stocks = df_factor.align(df_stocks, join='inner', axis=0)

Xf = df_factor.drop(columns=['RF'])

B=pd.DataFrame([],index=tickers,columns=Xf.columns)
for ticker in df_stocks.columns:
    y = df_stocks[ticker]
    X = sm.add_constant(Xf) 
    X=X[y.isna()==False]
    y=y[y.isna()==False]
    model = sm.OLS(y, X).fit(dropna=True)
    B.loc[ticker,:]=model.params[1:]

B

	Mkt-RF	SMB	HML	RMW	CMA	MOM
AAPL	1.030717	-0.107237	-0.008217	0.763479	-1.460115	-0.030158
GOOGL	0.958094	-0.470574	-0.210335	-0.1177	-1.148522	0.144696
MSFT	1.231883	-0.314873	0.077865	0.656917	-1.120852	0.093478
NVDA	1.2523	0.698145	-0.239075	0.321978	-0.472794	0.165622
AMZN	0.995541	-0.438021	0.05142	-0.267262	-2.001092	0.238466
COST	0.791177	-0.035685	0.006976	0.723471	0.02207	0.207055
WMT	0.77975	-0.139923	-0.256882	0.862723	0.496919	0.106942
TGT	0.863384	0.297708	-0.108899	1.244263	0.541671	0.099742
KR	0.740051	0.048948	-0.026441	0.274185	-0.074022	0.309473

Once we have the Asset betas, then we can compute the fund betas date by date by using the current composition of the portfolio

Obviously this allows you to track the exposure of the fund much better

matters a lot for funds that trade at very high frequency

_temp=final_portfolio_df.merge(B,left_on='ticker',right_index=True,how='left') 
Fund_B = _temp.groupby('date').apply(lambda x: pd.Series((x[Xf.columns].values * x['weight'].values.reshape(-1, 1)).sum(axis=0), index=Xf.columns))
Fund_B.plot()
display(Fund_B)

	Mkt-RF	SMB	HML	RMW	CMA	MOM
date
2014-12-31	1.093707	-0.126512	-0.065668	0.271483	-1.240675	0.122421
2015-01-01	1.093707	-0.126512	-0.065668	0.271483	-1.240675	0.122421
2015-01-02	1.093707	-0.126512	-0.065668	0.271483	-1.240675	0.122421
2015-01-05	1.093707	-0.126512	-0.065668	0.271483	-1.240675	0.122421
2015-01-06	1.093707	-0.126512	-0.065668	0.271483	-1.240675	0.122421
...	...	...	...	...	...	...
2016-12-26	0.793590	0.042762	-0.096312	0.776160	0.246659	0.180803
2016-12-27	0.793590	0.042762	-0.096312	0.776160	0.246659	0.180803
2016-12-28	0.793590	0.042762	-0.096312	0.776160	0.246659	0.180803
2016-12-29	0.793590	0.042762	-0.096312	0.776160	0.246659	0.180803
2016-12-30	0.793590	0.042762	-0.096312	0.776160	0.246659	0.180803

523 rows × 6 columns

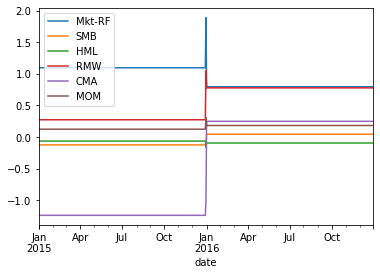
How do we estimate the fund abnormal return with this approach?

Note that there is no reason to believe that the asset betas as stable.

As we discussed, there is a lot of thought in deciding which sample is best to estimate the betas

• Long samples allow for more precision if the true beta is constant

• Shorter samples allow for you to capture time-variation

The general recipe that people use is 1-2 years when using daily data. 5 years when using monthly

13.8. The Cross-Sectional Approach ( or Characteristic-based model)

In the time-series approach, we start from the factors and estimate the betas

Now we will flip this: we will start from the betas–which are the characteristic–and use a regression to tell us what is the return associated with this characteristic

That is, we will estimate the factors themselves!

The time-series approach requires

• factors that are traded

• Need to estimate the time-series beta as a first step for abnormal return construction

The Cross-sectional approach goes directly from characteristics to abnormal returns and is often the preferred choice across quant shops because it allows for very large set of factors

The goal is to estimate the returns associated with a characteristic in a particular date, but do that in a way that does not involve the complicated steps of portfolio formation that are hard to do for many characteristics at the same time

Recipe

1. Get a large set of excess return for stocks (hopefully all) for a given date, R

2. Get the characteristics of these same stocks , X for this “date”.

• Important: the characteristics should be as of the the date before to avoid a spurious regression

• it is useful to normalize the characteristics so we can in terms of standard deviations from the average

3. Run the regression

\[R=BX+\epsilon\]

Note than from the OLS formula–If you have not seen this formula at some point in your life- today is the date!

\[B=(X'X)^{-1}X'R\]

• The B coefficients are excess returns themselves as they are just linear combinations of excess returns, i.e. the betas are portfolio returns

• They are returns on “pure play” portfolios. Portfolios designed to take a loading of 1 on a charateristic and zero in all the others

• \((X'X)^{-1}X'\) are the weights on the pure play portfolio

url = "https://github.com/amoreira2/Fin418/blob/main/assets/data/characteristics_raw.pkl?raw=true"

df_X = pd.read_pickle(url)
# This simply shits the date to be in an end of month basis


df_X.set_index(['date','permno'],inplace=True)
df_X


df_X

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Input In [1], in <cell line: 3>()
      1 url = "../../assets/data/characteristics_raw.pkl"
----> 3 df_X = pd.read_pickle(url)
      4 # This simply shits the date to be in an end of month basis
      7 df_X.set_index(['date','permno'],inplace=True)

NameError: name 'pd' is not defined

# lets standardize the data
X_std=(df_X.drop(columns=['re','rf','rme']).groupby('date').transform(lambda x: (x-x.mean())/x.std()))

#Lets start by picking a month
date='2006-09'
X=X_std.loc[date]
R=df_X.loc[date,'re']



# Run the regression
# multiplyin by 100 to get percentage
model = sm.OLS(100*R, X).fit()

# Print the summary of the regression
print(model.summary())

                                 OLS Regression Results                                
=======================================================================================
Dep. Variable:                     re   R-squared (uncentered):                   0.158
Model:                            OLS   Adj. R-squared (uncentered):              0.131
Method:                 Least Squares   F-statistic:                              6.017
Date:                Fri, 17 Jan 2025   Prob (F-statistic):                    1.81e-20
Time:                        10:42:57   Log-Likelihood:                          1301.8
No. Observations:                 962   AIC:                                     -2546.
Df Residuals:                     933   BIC:                                     -2404.
Df Model:                          29                                                  
Covariance Type:            nonrobust                                                  
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
size           0.0039      0.002      1.585      0.113      -0.001       0.009
value         -0.0276      0.008     -3.392      0.001      -0.044      -0.012
prof           0.0221      0.009      2.377      0.018       0.004       0.040
fscore        -0.0013      0.002     -0.579      0.563      -0.006       0.003
debtiss        0.0070      0.002      3.001      0.003       0.002       0.012
repurch        0.0029      0.002      1.234      0.217      -0.002       0.007
nissa         -0.0036      0.004     -0.987      0.324      -0.011       0.004
growth         0.0053      0.003      2.085      0.037       0.000       0.010
aturnover     -0.0026      0.012     -0.225      0.822      -0.026       0.020
gmargins      -0.0028      0.006     -0.444      0.657      -0.015       0.010
ep            -0.0031      0.003     -1.172      0.242      -0.008       0.002
sgrowth       -0.0018      0.002     -0.842      0.400      -0.006       0.002
lev            0.0337      0.006      5.485      0.000       0.022       0.046
roaa           0.0085      0.003      2.586      0.010       0.002       0.015
roea          -0.0031      0.003     -1.160      0.246      -0.008       0.002
sp            -0.0026      0.004     -0.656      0.512      -0.011       0.005
mom            0.0029      0.004      0.753      0.452      -0.005       0.010
indmom        -0.0116      0.002     -4.706      0.000      -0.016      -0.007
mom12         -0.0007      0.004     -0.198      0.843      -0.008       0.006
momrev        -0.0021      0.002     -0.923      0.356      -0.007       0.002
valuem         0.0144      0.008      1.895      0.058      -0.001       0.029
nissm          0.0016      0.004      0.445      0.657      -0.005       0.008
strev          0.0195      0.006      3.334      0.001       0.008       0.031
ivol          -0.0020      0.003     -0.615      0.539      -0.008       0.004
betaarb        0.0042      0.003      1.412      0.158      -0.002       0.010
indrrev       -0.0229      0.006     -4.084      0.000      -0.034      -0.012
price         -0.0021      0.002     -0.856      0.392      -0.007       0.003
age           -0.0044      0.002     -1.872      0.061      -0.009       0.000
shvol         -0.0032      0.003     -0.955      0.340      -0.010       0.003
==============================================================================
Omnibus:                       52.178   Durbin-Watson:                   1.910
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              137.505
Skew:                          -0.253   Prob(JB):                     1.38e-30
Kurtosis:                       4.782   Cond. No.                         16.9
==============================================================================

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

What this means?

• For example this means that a portfolio that takes one “unit” of the the size anomaly and zero of everything else had a return in that month of 0.39%

• Value got clobbered with a return of -2.76%

• Because we normalize, it means you have a portfolio that has stocks with 1 standard deviation of the characteristic above the characteristic average in that date

What are the portfolios?

#across lines we have the differnt characteristics and across columns we have the different stocks and their wights to implement the portfolio that is exposed to that chracteristic and nothign else

Characteristic_portfolio_weights=np.linalg.inv(X.T@X)@X.T
Characteristic_portfolio_weights

date	2006-09-30
permno	10104	10107	10137	10138	10143	10145	10147	10182	10225	10299	...	89702	89753	89757	89805	89813	90352	90609	90756	91556	92655
0	0.002726	0.004360	-0.000686	-0.000294	-0.001032	0.001538	0.001587	-0.000573	0.000838	-0.000320	...	-0.000651	-0.000082	0.002007	0.000279	0.001528	0.000292	0.000142	-0.000617	-0.000251	0.002837
1	-0.002632	0.006965	0.000676	0.000402	0.001094	0.000918	0.000914	0.001651	0.000402	0.000781	...	0.002959	-0.001872	-0.017175	-0.008553	-0.000069	0.007953	0.001755	-0.002131	-0.004422	-0.000381
2	-0.004929	-0.005258	0.002034	0.002285	-0.008617	0.002159	-0.000689	-0.001997	0.003331	-0.006068	...	-0.019083	0.002454	0.003818	0.001534	-0.017922	-0.005647	-0.000107	-0.002436	0.000742	0.002495
3	-0.000836	0.000893	-0.000555	-0.000177	0.002782	0.001506	0.002053	-0.000181	-0.001518	0.001342	...	0.000608	-0.000435	-0.001723	-0.000495	0.000966	-0.001019	-0.000310	0.001647	-0.000310	-0.000057
4	-0.001236	0.001006	-0.000597	0.000775	-0.000740	0.002011	-0.001833	0.001377	-0.000026	-0.000127	...	0.000919	0.000659	0.001524	-0.000626	-0.001255	-0.000257	0.001134	0.001364	0.001422	-0.000213
5	0.000264	-0.001071	0.001303	0.000584	0.002529	0.000491	0.000340	-0.001383	-0.001643	-0.000055	...	-0.000987	-0.001089	-0.002098	-0.001532	0.001370	0.000295	-0.002262	0.001152	0.000432	0.000759
6	-0.001617	0.000601	-0.000104	-0.000428	-0.002482	-0.000482	-0.000480	0.000256	-0.001693	0.000070	...	0.001202	0.000048	-0.002312	0.000341	0.000154	0.000719	-0.000753	-0.000134	-0.000160	-0.000975
7	0.002627	-0.002042	-0.001180	0.000641	0.006734	0.001257	0.000534	0.000382	0.002447	-0.000216	...	-0.000920	-0.000798	0.000595	0.000434	0.001237	-0.000225	0.000504	0.001170	0.000455	0.002122
8	0.004871	0.004464	-0.003664	-0.007132	0.007850	-0.000981	0.000484	-0.008215	-0.003439	0.002336	...	0.023270	-0.004813	-0.000239	-0.002821	0.022379	0.015255	0.000800	0.004665	0.001854	-0.001814
9	0.003855	0.004819	-0.002342	-0.003515	0.005676	-0.002311	0.000605	0.001060	-0.001483	0.003727	...	0.011010	-0.002337	-0.002309	-0.000579	0.010097	0.003309	0.001513	0.000325	-0.000946	-0.002444
10	0.000271	-0.000069	-0.000293	0.000143	-0.000826	-0.000250	-0.000066	0.006725	0.000147	0.000138	...	-0.000719	0.000504	0.000279	0.000525	-0.000788	-0.011986	0.000181	-0.001006	-0.000486	-0.000425
11	-0.000287	0.000121	0.000095	-0.000050	0.001933	0.000055	0.000081	-0.000231	-0.000377	0.000371	...	-0.000251	-0.000266	-0.000869	-0.000080	-0.000567	-0.001799	-0.000175	0.000012	0.000174	-0.000431
12	-0.001423	-0.001301	-0.001663	-0.005339	-0.005967	0.000626	-0.000846	-0.012928	-0.000303	-0.003485	...	0.002164	-0.002672	0.003537	0.000205	0.000187	0.009137	0.002843	0.002029	0.002139	0.000065
13	0.001069	0.001812	-0.000686	0.002124	-0.008606	-0.001630	-0.000170	-0.002489	-0.001095	0.002394	...	0.000023	0.000402	0.000735	0.001093	-0.001175	0.002575	0.002885	-0.000064	0.000134	-0.001065
14	-0.000707	-0.000298	0.000059	-0.000892	0.002531	0.000550	0.000388	0.000520	0.000250	-0.000938	...	0.000191	-0.000201	-0.001692	-0.000749	0.000008	0.000998	-0.000370	-0.000188	-0.000506	0.000377
15	0.000065	0.000296	-0.000223	0.002129	-0.000102	-0.000631	-0.000166	0.017161	-0.000159	0.001461	...	-0.002150	0.000303	-0.001075	0.000744	-0.001675	-0.011035	-0.000667	-0.001549	-0.001146	-0.000327
16	0.003275	-0.001444	0.000414	0.000814	0.004850	0.000500	-0.000680	-0.001967	0.001638	0.001538	...	-0.000963	0.006294	0.006965	0.000683	0.000819	-0.003108	-0.005419	-0.001557	-0.001139	-0.002296
17	-0.001036	-0.000790	0.001130	-0.000069	-0.000559	0.000744	0.001156	-0.000728	-0.003179	-0.000662	...	-0.000162	0.000246	0.000676	0.000207	-0.000602	0.001851	0.000070	0.001938	-0.000137	-0.000500
18	-0.000448	-0.000538	0.000771	0.000531	-0.003858	-0.001458	-0.000226	0.000581	-0.001932	-0.001952	...	-0.000535	-0.002585	-0.002551	0.002501	0.000042	0.001954	0.004019	0.001748	0.001367	0.001481
19	-0.000637	-0.000340	0.002424	-0.000383	-0.004906	-0.000384	-0.000023	-0.001467	0.000014	-0.000539	...	0.000848	-0.000252	0.002038	-0.002305	-0.000394	0.000808	-0.000372	-0.000406	-0.001321	0.000021
20	0.002454	-0.006450	-0.000259	0.000282	-0.000720	-0.001481	0.000044	-0.000981	-0.000074	-0.000625	...	-0.002613	0.003338	0.017058	0.007713	0.001418	-0.005177	-0.001665	0.001393	0.002914	-0.000042
21	0.001268	-0.001002	0.000261	0.000340	0.002121	0.000014	-0.000332	-0.001073	0.001485	-0.000074	...	-0.000455	0.000915	0.001289	0.002882	0.000152	0.001970	-0.001322	-0.000142	-0.000059	0.001160
22	0.001438	0.000856	0.001983	-0.003842	-0.001651	-0.005159	0.008296	-0.001921	-0.000597	0.003292	...	0.000462	0.001209	0.000576	-0.000857	-0.000587	-0.007146	0.001954	0.002193	-0.002015	0.001781
23	-0.000693	-0.000813	-0.000575	-0.000243	-0.000003	-0.000482	0.000029	-0.001962	0.000155	-0.002279	...	-0.001825	0.002788	-0.000676	-0.001814	0.000046	-0.000871	-0.001244	0.000096	-0.001520	0.000576
24	0.001033	-0.001787	-0.000101	0.002654	0.001072	0.002249	0.000876	0.000410	-0.000529	0.001736	...	0.000448	0.001858	0.002971	-0.000773	0.000476	0.002359	-0.000862	-0.000513	-0.000372	-0.002154
25	-0.000593	-0.000945	-0.001676	0.004517	0.003180	0.004748	-0.007188	-0.000257	0.000174	-0.003453	...	-0.000215	0.000768	0.001334	0.001912	0.001349	0.008045	-0.002434	0.000882	0.001426	-0.000810
26	-0.002615	-0.001900	-0.000078	0.000075	0.001128	-0.000128	-0.001855	0.000754	0.001165	0.000277	...	0.001324	0.001663	0.003084	-0.001295	0.000703	-0.002491	-0.003785	0.000367	-0.001120	-0.000556
27	0.000211	-0.000759	0.001319	0.000274	0.002850	0.000730	-0.000111	-0.000180	0.001711	0.000712	...	-0.002721	-0.001921	-0.003869	-0.002800	-0.003422	-0.002200	0.000486	0.000351	-0.000007	-0.000230
28	-0.000060	0.001666	0.000600	-0.002817	0.002260	-0.001090	0.000591	-0.000607	-0.000647	0.001927	...	0.000396	-0.000141	-0.000070	-0.000177	-0.001354	-0.000996	0.000648	-0.000197	0.000323	-0.000739

29 rows × 962 columns

What do we do with this?

1. For a give portfolio I can exactly compute it’s charaterestic-adjusted portfolio returns

2. I can also construct a time-series of return for each characteristic, by simply splicing together the regression coefficients of different dates.

• Essentially I would run a for loop and get a sequence of betas \([\beta_t,\beta_{t+1},...]\) and these would be the returns on the factors

13.8.1. Constructing Characteristic adjusted returns

We can get the portfolio characteristics and based on that construct the return implied by these characteristics

We then subtract these characteristic returns from the portfolio returns

It is the equivalent of the “hedged portfolios” that uses the betas to hedge. Here we simply use the characterisitc–instead of makign “factor” neutral we make them characteristic neutral

Are these the same thing?

# Step 1: construct 2 portfolios 1 and 2 ( tech and retail)

portfolio_data1 = {'port': [1,1,1,1,1],
    'ticker': ['AAPL', 'GOOG', 'MSFT','NVDA','AMZN'],
    'weight': [0.2,0.2, 0.2,0.2,0.2]
}

portfolio_data2 = {'port': [2,2,2,2],
    'ticker': ['COST', 'WMT', 'TGT','KR'],
    'weight': [0.25,0.25, 0.25,0.25]
}

portfolio_df1 = pd.DataFrame(portfolio_data1)
portfolio_df2 = pd.DataFrame(portfolio_data2)
portfolio_df = pd.concat([portfolio_df1, portfolio_df2], ignore_index=True)
print(portfolio_df)

C:\Users\Alan.Moreira\AppData\Local\Temp\ipykernel_42500\2476330753.py:13: FutureWarning: The frame.append method is deprecated and will be removed from pandas in a future version. Use pandas.concat instead.
  portfolio_df=portfolio_df1.append(portfolio_df2)

WRDS recommends setting up a .pgpass file.
Created .pgpass file successfully.
You can create this file yourself at any time with the create_pgpass_file() function.
Loading library list...
Done

	permno	ticker	namedt	nameenddt
276	10107	MSFT	1986-03-13	2023-12-29
9575	14542	GOOG	2014-04-03	2015-10-04
9576	14542	GOOG	2015-10-05	2023-12-29
9663	14593	AAPL	1980-12-12	2007-01-10
9664	14593	AAPL	2007-01-11	2023-12-29
13089	16678	KR	1962-07-02	1968-01-01
13090	16678	KR	1968-01-02	2023-12-29
25347	25225	COST	1972-12-14	1979-07-10
26009	26542	TGT	1962-07-02	1966-04-12
26010	26542	TGT	1966-04-13	1968-01-01
26011	26542	TGT	1968-01-02	1995-04-02
35981	49154	TGT	2000-01-31	2002-01-01
35982	49154	TGT	2002-01-02	2023-12-29
38700	55976	WMT	1972-11-20	2002-01-01
38701	55976	WMT	2002-01-02	2012-02-29
38702	55976	WMT	2012-03-01	2014-01-06
38703	55976	WMT	2014-01-07	2018-01-31
38704	55976	WMT	2018-02-01	2020-11-17
38705	55976	WMT	2020-11-18	2023-12-29
64248	84788	AMZN	1997-05-15	2023-12-29
67507	86580	NVDA	1999-01-22	2023-12-29
68257	87055	COST	1985-11-27	1993-10-21
68259	87055	COST	1997-02-06	1998-08-31
68260	87055	COST	1998-09-01	1999-08-29
68261	87055	COST	1999-08-30	2023-12-29
74136	90319	GOOG	2004-08-19	2014-04-02

# Step 2: Get the permnos associated with these ticker so we can do the matching
# our data has permnos, not tickers
conn=wrds.Connection()
# get the pemnos for the tickers
permno=get_permnos(portfolio_df.ticker.unique(),conn)

permno['namedt'] = pd.to_datetime(permno['namedt'])
permno['nameenddt'] = pd.to_datetime(permno['nameenddt'])

date='2008-03'
d = pd.to_datetime(date)
# note that sometimes the pernmo changes!
# so we need to get the permnos that are valid at the relevant date
permno_d=permno[(permno['nameenddt']>=d) & (permno['namedt']<=d)]

portfolio_df=portfolio_df.merge(permno_d[['permno','ticker']],on='ticker',how='left') 
portfolio_df

# Step 3: merge our portfolio with our main data set that contains returns and characterisitc
# here we are doign just for one date. Of course you can also do for multiple dates. 
#IF the portfolios are fixed that is trivial. If the portfolio is changing , then you should have two identifiers for your
#portfolio in step 1 "port" and "date"


X=X_std.loc[date].reset_index()
port_stocks_X=portfolio_df.merge(X,left_on='permno',right_on='permno',how='left')
port_stocks_X

c:\Users\Alan.Moreira\Anaconda3\lib\site-packages\pandas\core\ops\array_ops.py:73: FutureWarning: Comparison of Timestamp with datetime.date is deprecated in order to match the standard library behavior. In a future version these will be considered non-comparable. Use 'ts == pd.Timestamp(date)' or 'ts.date() == date' instead.
  result = libops.scalar_compare(x.ravel(), y, op)

	port	ticker	weight	permno	date	size	value	prof	fscore	debtiss	...	momrev	valuem	nissm	strev	ivol	betaarb	indrrev	price	age	shvol
0	1	AAPL	0.20	14593	2008-03-31	2.410205	-1.315480	0.455224	-0.091077	1.303219	...	0.575718	-1.421058	0.147848	-0.580727	0.330686	0.752957	-0.868990	1.888114	0.398208	2.904418
1	1	GOOG	0.20	90319	2008-03-31	2.528013	-1.118659	0.564933	-0.091077	1.303219	...	0.755154	-1.005315	0.229125	-1.402481	0.158169	-0.694430	-1.224557	3.959159	-2.339689	1.693268
2	1	MSFT	0.20	10107	2008-03-31	3.257090	-1.363239	0.985259	0.755457	1.303219	...	0.726842	-1.531135	-0.438239	-1.377024	-0.637930	-0.456596	-1.195484	-0.492776	0.105671	-0.399737
3	1	NVDA	0.20	86580	2008-03-31	0.680226	-1.634531	0.817117	0.755457	1.303219	...	1.172971	-0.842731	0.223491	-1.079041	1.603828	2.812533	-1.183732	-0.867861	-1.084778	1.545659
4	1	AMZN	0.20	84788	2008-03-31	1.240524	-3.728875	1.118980	-0.091077	1.303219	...	1.249185	-3.528315	0.034269	-1.451173	0.544068	1.264655	-1.341326	0.854323	-0.858657	1.347997
5	2	COST	0.25	87055	2008-03-31	1.154301	0.138992	0.785716	-0.091077	-0.766462	...	-0.499439	-0.268807	-0.301382	-0.674229	-0.579135	-0.414050	-0.454017	0.791327	0.126212	0.223698
6	2	WMT	0.25	55976	2008-03-31	2.960595	-0.322603	1.029022	-0.937610	-0.766462	...	-0.424544	-0.260600	-0.348921	-0.082608	-1.065065	-0.802397	0.221643	0.444707	0.753804	-1.140483
7	2	TGT	0.25	49154	2008-03-31	1.815796	-0.209013	0.909948	1.601991	-0.766462	...	0.974779	-0.055104	-0.423087	-0.319158	0.450388	0.077535	-0.048508	0.536987	0.871398	0.443988
8	2	KR	0.25	16678	2008-03-31	0.934108	-0.149013	1.326149	0.755457	-0.766462	...	-0.172023	-0.295956	-0.406029	-0.282320	-0.487468	-0.728124	-0.006437	-0.671970	1.220560	-0.344465

9 rows × 34 columns

Now we can compute each portfolio characteristic

# step 4: finally we simply average the characteristics within each portfolio
# we now know how value, momentum, and so on is our portfolio as a funciton of what they hold

X_names=X.drop(columns=['permno','date']).columns
port_X=port_stocks_X.groupby('port').apply(lambda x: x['weight'] @ x[X_names])
port_X

We can then compute the portfolio “characteristic-implied” returns and the portfolio characteristic-adjusted return

# Step 5:  estimate the return associated with each characteristic  using the entire investment universe
# we already this step above, but I am repeating here for completeness
# you eould have to repeat this procedure date by data if doign that for multiple dates

X=X_std.loc[date]
R=df_X.loc[date,'re']

# Run the regression
model = sm.OLS(R, X).fit()

R_X=model.params
R_X

port
1   -0.027497
2    0.006339
dtype: float64
port
1    0.029733
2    0.030074
dtype: float64
port
1    0.057230
2    0.023735
dtype: float64

# Step6: compute the charateteristic implied returns by using the portfolio chanrateristics to compute the portfolio returns
#implied by these characteristics. This the equivalent of $\sum \beta f_{t}^i$, but here port_X are the "betas" 
# and R_X and the factors--the returns associated with the charateristic 

port_characteristic_returns=port_X[X_names] @R_X
print(port_characteristic_returns)

# step 7: Subtract the charateristic implied return from the portfolio return to obtain the charateristic-adjsuted retrun
# this is the equivalent of $R^{port}_t-\sum \beta f_{t}^i$

# portfolio  raw excess return
_temp=portfolio_df.merge(R.reset_index(),left_on='permno',right_on='permno')
R_port=_temp.groupby('port').apply(lambda x: x['weight']@ x['re'])
print(R_port)

#  characteristic-adjsuted
Port_characteristic_adjsuted_returns=R_port-port_characteristic_returns
print(Port_characteristic_adjsuted_returns)

Why practitioners like this?

• You don’t need the time-series betas and all the issues with the size of the sample and how they might move around

• All you need is the characteristic at a given date, and that characteristic can move around a lot as we estimate date by date

• We used no time-series data at all

• You can have very large number of factors: can add sector/industry factors, country factors, currency factors, you name it. Just add to your regression

What are the issues?

• The main issue is that ignores covariances, so the characteristic-adjusted portfolios are characteristic neutral but not factor neutral

  • For example: a stock might be large but co-move with small stocks and not large stocks, a stock might be classified as retail but co-move with tech

  • of course we only care about the characteristics because they describe movement in returns

  • But this might or might not be true and we re almost certain that it will be suboptimal

  • Now as the number of characteristics grow and they describe returns better and better, this becomes less of an issue

  • Consistent with the industry practice of have large set of characteristics (often north of 50-100)

• Another issue is that this approach will tend to load on small stocks

  • Basically the OLS tries to fit all data points equally and most stocks are tiny

  • One fix is to use Weighted-Least Squares where you put more weight on larger firms

  • or simply estimate your characteristic returns eliminating the smallest stocks–say focus on the top 20% by market cap

---

📝 Key Takeaways

• Multi-factor models are the industry work-horse. They capture multiple rewarded risks simultaneously, delivering more realistic benchmarks and richer performance attribution.

• Alpha is scarce; beta is plentiful. Time-series regressions on standard factors reveal that most “smart-beta” ETFs provide factor exposure, not out-performance—true skill shows up only in the intercept.

• Variance decomposition sharpens intuition. Viewing risk as a weighted blend of factor volatilities highlights which exposures dominate and where diversification gains remain.

• Factor-based covariance matrices are stabler and more tractable. Using a handful of factors plus idiosyncratic terms avoids the noise that plagues full empirical covariances, improving minimum-variance and risk-parity constructions.

• Risk changes with allocation tilts, not just position size. A small weight shift toward a fund with similar betas barely moves portfolio volatility, while the same shift toward a factor-orthogonal fund can raise risk sharply.

• Bottom-up attribution excels for high-turnover managers. Refreshing exposures at the holding level avoids the lag and instability that afflict purely return-based estimates.

• Characteristic models broaden the toolkit but ignore covariances. They neutralize portfolios on observed attributes quickly and at scale, yet leave hidden co-movement risks untouched—reminding practitioners that factor and characteristic views are complements, not substitutes.

---